How do you approach this conundrum? My background is not in Mathematics but I am willing to learn.
QUESTION:
Given this equation:
$$ y = c * sin\theta - r * \theta*sin\theta - r * cos\theta;\ where \begin{cases} y = variable\\ c = fixed\ length \\ r = radius \\ \theta = angle\ in\ radians \end{cases} $$
How do you find $\theta_1$ given $y_1$?
BACKGROUND:
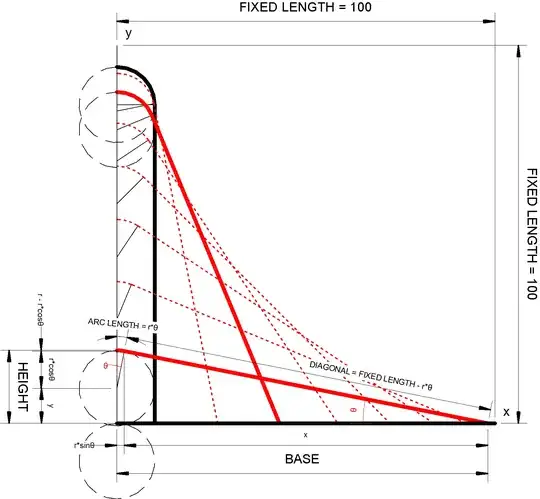
I am ultimately trying to solve this diagram: Get $x$ when given $y$
Where the following constraints must be satisfied:
- The length of red lines ($ARC LENGTH + DIAGONAL$) must equal the $FIXED \ LENGTH$.
- As the $HEIGHT$ increases, the $BASE$ decreases.
- The maximum ${HEIGHT}$ is given by the equation: $$ HEIGHT_{max} = (FIXED\ LENGTH - r*\fracπ2) + r $$ at which point $${BASE}_{min} = r $$
The minimum ${HEIGHT}$ is given by the equation: $$ HEIGHT_{min} = 0 $$ at which point $${BASE}_{max} = FIXED\ LENGTH$$
The red lines must always start at $x=0$, rotate over a circle of radius $r$, and end at $y=0$ (it must always be attached to the $x-$ and $y-axis$).
- As such, $r$ and $FIXED\ LENGTH$ are constants
- $\theta$ is dependent on $y$ .
WHAT HAS BEEN DONE:
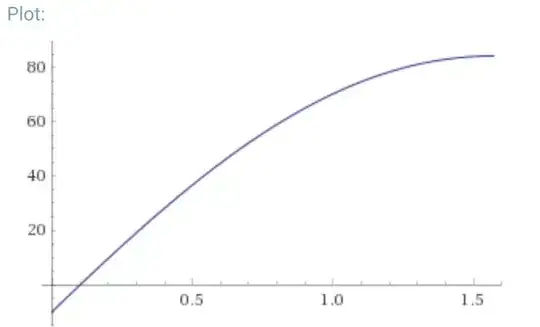
When $\theta$ is given, it is relatively easy to find $y$. For example for the cases:
$$ \begin{cases} y = variable\\ c = 100 \\ r = 10 \\ \theta = 0\ to\ \fracπ2 \end{cases} $$
This is a plot of all the possible values for $\theta$ and $y$.
WHAT I AM LOOKING FOR (FOLLOW-UP):
I know that the function is an oscillating function, and that for each value of $y$, there are numerous values for $x$. However, I am only looking for the specific range where $\theta = 0\ to\ \frac\pi2$ and $y = -r\ to\ c-r\frac\pi2$.
If finding $\theta_1$ given $y_1$ is not possible, these are my follow-up questions:
- How can the problem be viewed differently?
- How should the problem be approached?
- What concepts are needed to solve these types of problems?
- any technical terms for what these types of problem are?
- what branches of mathematics are useful for understanding these types of problems?
DISCLAIMER:
- This problem is for a "fun" side project and I am stuck on the mathematics side since I absolutely have no background about the advanced branches of mathematics needed for this.
- If you can suggest tags or better ways to phrase this question. Please do not hesitate to point it out. Thanks.