As I have research so far we cannot solve arbitrary polynomial by radical
But as I was scope my work. I found out that I have only need to find inverse function for a specific kind of polynomial
I have to create a polynomial from a number of points. The curve from this polynomial must pass all these point. And it must pass each point with tangent 0, which means derivative of function at that point must be 0
And so I can find the coefficient of polynomial by systems of equation
Suppose I define that, the function would pass at trivial point 0,0 and 1,1. Then it must pass point 0.5,0.5 with tangent 0
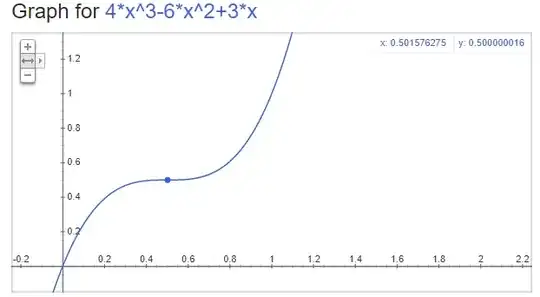
I then got this equation $y = 4x^3 - 6x^2 + 3x$
Which produce this curve
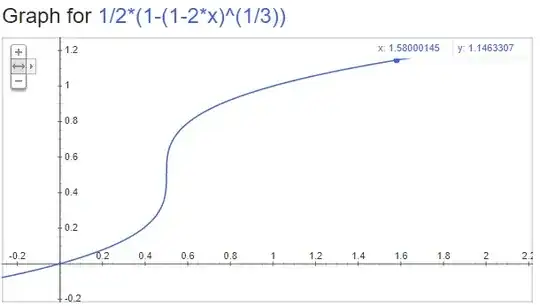
And so I got this inverse function $y = \frac{1}{2}(1 - \sqrt[3]{1-2x})$ which produce
And the curve only grow in one direction without decrease. What I made is actually a smooth step function. So the inverse of the function is also the function and always has root in every degree
I could make these kind of polynomial from any number of points in any degree for approximate the step function. But I want to find inverse function for all of it
So, given these restriction, is there a formula to inverse these kind of polynomial in any degree?