$\tan{A} \cdot \tan{B} \cdot \tan{C}=9$, find $\tan^2{A}+\tan^2{B}+ \tan^2{C}$

Question

In $\triangle{ABC}$,

$$\tan{A}\cdot \tan{B}\cdot \tan{C}=9$$

$$\tan^2{A}+\tan^2{B}+ \tan^2{C}=\lambda$$

then,

$\lambda$ lies in the interval?

Answer 1

As lab bhattacharjee noted in comments, for triangle angles we have $$\tan A\cdot \tan B \cdot \tan C = \tan A + \tan B + \tan C.\tag{1}$$

Denote $\;\;x=\tan A,\quad y=\tan B, \quad z=\tan C$.

We have $$x+y+z=9;\\ xyz=9;\tag{2}$$ and we try to estimate expression $$x^2+y^2+z^2.$$

Let use $z$ as parameter ($0<z<9$). Then $$x+y=9-z;\\ xy=9/z;$$ and we try to estimate expression $$(x^2+y^2)+z^2=(x+y)^2-2xy+z^2=(9-z)^2-\dfrac{18}{z}+z^2.\tag{3}$$

Now, $x$ and $y$ (according to Vieta's theorem) are solutions of quadratic equation $$a^2-(9-z)a+\dfrac{9}{z}=0.\tag{4}$$ This equation has (real) positive solutions if $(9-z)^2z\ge36$.

So, bounds for $z$ are (approximately): $$z\in I, \mbox{ where } I=[0.498040,6.678221].\tag{5}$$

Considering expression $(3)$ on segment $(5)$, we reach minimal value when $z\approx 4.25098$: $$\min_{z\in I}\{x^2+y^2+z^2\}\approx 36.3897;\tag{min}$$ and we reach maximal value when $z\approx 6.678221$: $$\max_{z\in I}\{x^2+y^2+z^2\}\approx 47.29396.\tag{max}$$

Minimizing parameters: $x \approx 0.4980402$, $y=z\approx 4.250979.$

Maximizing parameters: $x =y\approx 1.160889$, $z\approx 6.678221.$

---

This result can be obtained using Lagrange multipliers as well.

Answer 2

Since $A+B+C=\pi$, we have $$ \tan(A)\tan(B)\tan(C)=\tan(A)+\tan(B)+\tan(C)\tag1 $$ Letting $x=\tan(A)$, $y=\tan(B)$, and $z=\tan(C)$, our constraints become $$ x+y+z=xyz=9\tag2 $$ Solving for $y\ge z$ in terms of $x$, we get $$ y=\frac{x(9-x)+\sqrt{x^2(9-x)^2-36x}}{2x}\tag3 $$ and $$ z=\frac{x(9-x)-\sqrt{x^2(9-x)^2-36x}}{2x}\tag4 $$ Then, we get $$ \begin{align} s(x) &=x^2+y^2+z^2\\ &=\frac{3x^3-18x^2+81x-18}{2x}\tag5 \end{align} $$ and $$ s'(x)=3x-9+\frac9{x^2}\tag6 $$ and $$ s''(x)=3-\frac{18}{x^3}\tag7 $$ where we need $$ d(x)=x^2(9-x)^2-36x\ge0\tag8 $$ so that $y,z\in\mathbb{R}$. $d(x)\ge0$ on $$ (-\infty,0],[0.498040209888,6.678221141368],[10.823738648744,\infty)\tag9 $$ If any of $x,y,z\lt0$, since $xyz=9$, exactly two of $x,y,z\lt0$, but this would imply two obtuse angles. Thus, $x,y,z\gt0$. If $x\gt9$, then $y+z\lt0$. Therefore, we can only have $$ 0.49804020988787915596\le x\le6.6782211413676239727\tag{10} $$

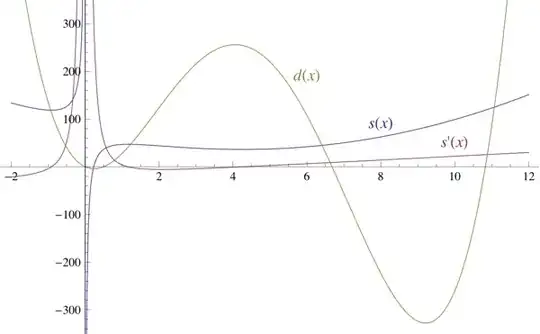
Formula $(5)$ has one local maximum at $$ \begin{align} x&=1.1608894293161880136\\ x^2+y^2+z^2&=47.29396614720561963\tag{11} \end{align} $$ and one local minimum at $$ \begin{align} x&=4.2509798950560604220\\ x^2+y^2+z^2&=36.38970418700683168\tag{12} \end{align} $$ We also have the two edge cases $$ \begin{align} x&=0.49804020988787915596\\ x^2+y^2+z^2&=36.38970418700683168\tag{13} \end{align} $$ and $$ \begin{align} x&=6.6782211413676239727\\ x^2+y^2+z^2&=47.29396614720561963\tag{14} \end{align} $$ Therefore, under the conditions given, we have $$ \bbox[5px,border:2px solid #C0A000]{36.38970418700683168\le x^2+y^2+z^2\le47.29396614720561963}\tag{15} $$

Answer 3

We have the inequality $\displaystyle (ab+bc+ca)^2 \ge 3abc(a+b+c)$

Also in $\displaystyle \triangle ABC, \ \tan A+\tan B + \tan C = \tan A \tan B \tan C$,

Hence, $\displaystyle \left(\sum \tan A \tan B \right)^2 \ge 3 \times 9^2 \Rightarrow \sum \tan A \tan B \notin \left(- 9 \sqrt 3 , 9 \sqrt 3 \right)$

So $\displaystyle \sum \tan^2 A = \left(\sum \tan A \right)^2 - 2 \sum \tan A \tan B \notin (81-18 \sqrt 3, 81+18 \sqrt 3)$