4

I am currently trying to construct a vector in space given yaw, pitch, and roll with the assumption that my ray originates from (0,0,0).

I started by breaking up the problem into 3 sets of triangles by slicing space in 3 ways:

  • In the X-Y plane, I concluded that x = sin(yaw) and y = cos(yaw)
  • In the Y-Z plane, I determined that y = cos(pitch) and z = sin(pitch)
  • In the X-Z plane, I found that x = cos(pitch) and z = sin(pitch)

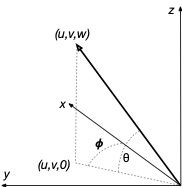
From this, I arrived at enter image description here

However, this doesn't seem to satisfy basic tests, such as <1,1,1>, where the Yaw = Pi/4 and the Pitch should be Pi/4, but the formula yields 0.5, 0.5, 0.7, which has a direction vector different than <1,1,1>. Can anyone spot where I messed up? I've been banging my head at this for a while, and I can't seem to resolve where I made an error.

user1939991
  • 181
  • The yaw is $\pi/4$ but the pitch is $\arcsin(1/\sqrt{3}).$ – wcochran Nov 23 '19 at 00:59
  • Usually when we mention "roll" we're interested in more than just the "straight ahead" vector, so if you're interested in this question, questions like https://math.stackexchange.com/questions/1637464/find-unit-vector-given-roll-pitch-and-yaw may also have useful answers. – David K Nov 23 '19 at 03:03

1 Answers1

3

enter image description here

I'll use the OMAF coordinate system which defines the viewer looking out the $x$-axis with $z$-axis up and the $y$-axis to the left. Given a yaw angle $\phi$ and a pitch angle $\theta$ we transform the direction vector $(u,v,w)$ onto the view axis $(1,0,0)$ by first performing a clockwise rotation about the $z$-axis by $\phi$ followed by a counter-clockwise rotation about the $y$-axis by $\theta:$ $$ \left[\begin{array}{c}1\\0\\0\end{array}\right] = R_y(\theta) \cdot R_z(-\phi) \left[\begin{array}{c}u\\v\\w\end{array}\right] $$

We then solve for $(u,v,w)$ and get $$ \left[\begin{array}{c}u\\v\\w\end{array}\right] = R_z(\phi) \cdot R_y(-\theta) \left[\begin{array}{c}1\\0\\0\end{array}\right] $$

$$ \left[\begin{array}{c}u\\v\\w\end{array}\right] = \left[\begin{array}{ccc}\cos\phi & -\sin\phi & 0 \\ \sin\phi & \cos\phi & 0\\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{ccc}\cos\theta & 0 & -\sin\theta \\ 0 & 1 & 0 \\ \sin\theta & 0 & \cos\theta \end{array}\right] \left[\begin{array}{c}1\\0\\0\end{array}\right] = \left[\begin{array}{c}\cos\phi\cos\theta \\ sin\phi \cos\theta \\ \sin\theta \end{array}\right] $$

which is your classical spherical to cartesian transformation where $\phi$ is the azimuthal angle and $\theta$ is the elevation angle. Note that the roll angle does not enter into the equation since it merely defines a rotation about the direction vector which does not alter the direction vector.

If you happen to be using OpenGL conventions where the viewer is looking out the $-z$-axis and the $y$-axis is "up" and the $x$-axis is to the right you will use the direction $(u',v',w') = (-v,w,-u).$

wcochran
  • 720
  • Interestingly, OP's final formula turns out to be correct for a right-handed system with $z$ pointing up if you measure yaw clockwise (as many people do) and you are initially pointing in the direction $(0,1,0).$ Since the assumptions are missing from the question, it's hard to say if this was the desired result, but I think your comment under the question was the answer to what I took to be the main question, "Can anyone spot where I messed up?" – David K Nov 23 '19 at 03:02