4

This post is mainly concerned about

$$2^{107} \pmod {187} \equiv 161$$

enter image description here

being quickly or immediately solvable. Far from being my problem, I took it as an exercise in applying, as slowly as possible, the CRT after my own post yesterday on the topic. The intermediate results are verified with WolframAlpha to focus on the important points.

Unfortunately something is incorrect in my application, and sorting it out can help shed some additional light on the CRT and related theorems.

Following @lulu's tip, i.e. $187=11\times 17:$

$2^{107}\equiv 7 \pmod{11}$ since applying Euler's theorem,

$2^{\phi(11)}=2^{10}\equiv 1 \pmod{11}.$ Therefore,

$2^{107}\pmod{11}=\left(2^{10}\right)^{10}\cdot 2^7\pmod{11}\equiv2^7\pmod{11}\equiv \color{red}7\pmod {11}.$

enter image description here

And

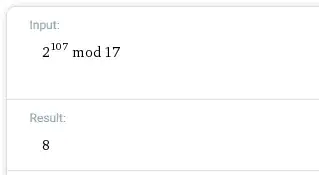
$2^{107}\equiv 8 \pmod{17}$ since applying Euler's theorem,

$2^{\phi(17)}=2^{16}\equiv 1 \pmod{17}.$ Therefore,

$2^{107}\pmod{17}=\left(2^{16}\right)^{6}\cdot 2^{11}\pmod{17}\equiv2^7\pmod{11}\equiv \color{blue} 8\pmod {17}.$

enter image description here

Applying now the formula of the CRT:

$$x\equiv a_1 b_1 \frac{M}{m_1}+a_2 b_2 \frac{M}{m_2}\pmod M$$

first by calculating

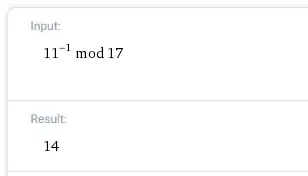
$b_1 = (187/11)^{-1}\pmod{11}\equiv\color{red}2\mod{11}$

enter image description here

and

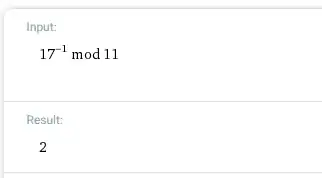
$b_2=(187/17)^{-1}\pmod{17}\equiv\color{blue}{14}\mod{11}$

enter image description here

it would seem that

$2^{107}\pmod{187}=\color{red}7\cdot \color{red}2\cdot17 + \color{blue}8\cdot\color{blue}{14} \cdot11\equiv1470 \pmod{187}$

which is not the expected 161.

Where have I missapplied the CRT?

Jaideep Khare
  • 19,293
Antoni Parellada
  • 8,889

3 Answers3

5

Since $1470= 7 \cdot 187 + 161$ ; $$1470 = 161\pmod{187}$$

Jaideep Khare
  • 19,293
  • I see, I see... I should have checked... Is this an exercise expected to be carried out each time one uses the CRT? To further reduce the result to the lowest congruent number? – Antoni Parellada Jan 22 '18 at 17:49
  • 3
    Not only CRT, everytime, for checking congruences. – Jaideep Khare Jan 22 '18 at 17:50
  • 3
    Did the question ask for the least positive integer? If not, $1470$ is not incorrect. However, it should be obvious that $1470 > 187$ (that's a no brainer) so if that if the book solution was $161$ the first thing you should assume is $1470 \equiv 161 \mod 187$ (although you should double check with a calculator). BTW many text and courses would prefer $-26$ as an answer (as long as we are worrying about "mere" representation) – fleablood Jan 22 '18 at 17:56
  • True.... I was assuming it was clear in context. Perhaps I shouldn't have. – fleablood Jan 22 '18 at 18:03
  • @fleablood Am I missing something? – Jaideep Khare Jan 22 '18 at 18:04
  • What? No. I was responding to shouldn't be here's question "s this an exercise expected to be carried out each time one uses the CRT? To further reduce the result to the lowest congruent number?" The correct answer to the question is $1470_{187}$ which is the same valus as $161_{187} = -26_{187} = 348_{187}= etc.$. If the question didn't ask for the least positive value the answer IS $1470$. Which IS the SAME answer as $161$. But it SHOULD be apparent to a student that $1470 \equiv 161 \equiv -26 \mod 187$ and that they are both the SAME answer. – fleablood Jan 22 '18 at 18:18
  • @fleablood Ok. ${}{}{}{}{}{}{}{}{}{}{}{}$ – Jaideep Khare Jan 22 '18 at 19:03
3

Your result is correct since $1470\equiv 161 \mod187$.

The class representative$\mod n$ is unique only if you take it to be non negative and less than $n$.

Arnaud Mortier
  • 27,276
  • 2
    " class representative is unique only if you take..." I think it is important to note that although the class representation is not unique, but that the class itself, $[161] = {...., -26, 161, 348, ....., 1283, 1470, 1657, ....}$ is unique. ( $[161] = [-26] = [348] = [1470] = .... etc.$ are all different ways of expressing the one unique thing.) – fleablood Jan 22 '18 at 18:01
  • 1
    Once you've fixed one representative per class, by construction the class representative will be unique. On the other hand, the standard set of representatives for congruence classes modulo $n$ is ${0,1,\dotsc,n-1}$. – A.P. Jan 23 '18 at 00:04
3

As already observed, $1470\equiv 161 \bmod 187$ so to equivalence you already had the right answer for $E:=2^{107} \bmod 187$.

You could end up a lot closer in the initial calculation by using $11^{-1} \equiv -3 \bmod 17$ (which I would find from $3\cdot 11 =33 \equiv -1 \bmod 17$). This gives your calculation as

$E \equiv7\cdot2\cdot17 + 8\cdot(-3) \cdot11 = -26 \equiv 161 \pmod{187}$

I find it useful being comfortable with using the small negative instances of a residue class.

The other simple/simplistic approach to solving the CRT portion is simply to search the space of solutions. You know that

$\begin {cases} E\equiv 7 \bmod 11 \\ E\equiv 8 \bmod 17 \end{cases}$

Then you can check the values in range for the $\bmod 17$ criterion formed by $8{+}17k$, that is $\{8,25, 42, 59, 76, 93, 110, 127, 144, 161, 178 \}$, to find which one meets the $\bmod 11$ criterion also.

Following on from this, you could also directly solve for $k$ in $8 + 17k\equiv 7 \bmod 11$:

$\begin{align} 8 + 17k&\equiv 7 \bmod 11\\ 6k &\equiv -1 \bmod 11\\ 2\cdot6k &\equiv -2 \equiv 9\bmod 11\\ 12k \equiv k &\equiv 9 \bmod 11\\ \end{align}$

Then $8+17\cdot 9 = 161$.

Joffan
  • 39,627