Proof Verification: $1 \leq x^2 + y^2 \leq 2$ is connected?

Question

Initutively it's super obvious that it's connected. My formal proof goes this way: $x^2 + y^2 = 1$, $ y = mx$ and $x^2 + y^2 = 2$ are connected. Since any point in the region lies in $y = mx$, and $y = mx$ intersects both $x^2 + y^2 = 1$, $ y = mx$ and $x^2 + y^2 = 2$, we use the theorem that "if conneted subpaces has a common point, then their union is connected" to conclude that the whole region is connected. But I think my proof is not elegant and I suspect their exist a simplier reasoning than I used, so I would like to know if that is really the case.

Answer 1

Consider the square $[1,2]\times [0,2\pi]$. This is connected because real intervals are connected (proof) and cartesian product of connected spaces is connected (proof). Since your space is the image of the continuous function $$(r,\theta)\in[1,2]\times [0,2\pi]\mapsto (r\cos(\theta),r\sin(\theta))$$ it's connected because the image of a connected space through a continuous function is connected (proof).

Answer 2

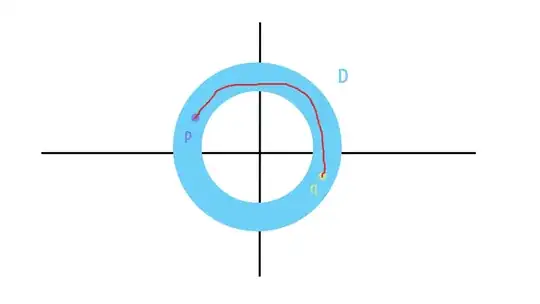
Let $D = \{ (x, y) \ | \ 1 \leq x^2 + y^2 \leq 2\}$ denote the disk.

Observe that for any two points $p, q$ in $D$ there exists a path (a continuous function) $\gamma : [0, 1] \to D$ such that $\gamma(0) = p$ and $\gamma(1) = q$. You only need to draw a picture like the one below to convince yourself of this fact. Note that the red line is the graph of the path $\gamma$.

Hence $D$ is path connected, and thus connected.

---

In general it is much easier to verify path-connectedness and then use that to prove connectedness, so where you can try and follow this approach.

Answer 3

Show that it is path connected.

Pick two points $A$ and $B$ in your set.

As you mentioned in your proof, you can go from A to the inner boundary via a segment of $ y=m_1 x$ and trace the circle to get to $ y=m_2 x$ which contains $B$

I am sure that you can fill in the details.

Answer 4

The other answers have given you ideas of how to write a correct proof, but no one has yet addressed the correctness of your proof!

Unfortunately your proof is incorrect for a number of reasons, although there are some correct aspects to your reasoning. You talk about points lying in $y = mx$, which is not a correct way of stating the idea that your points lie in a line. Note that $y = mx$ is an equation, not a set; I think you mean $\{(x, y) : y = mx\}$. Of course, you need to preceed this by saying what $m$ is! You've never defined it, and you really should.

The next issue is that lying in a line is not enough to guarantee connectedness; take $[0, 1] \cup [2, 3]$ for example. And the intersection of a line $y = mx$ with your region is not connected - it's a union of two line segments.

The final issue that I'll point out is that even if you take the union of your lines over $m \in \mathbb{R}$, you're missing (almost) all the points on the $y$-axis.