I'm trying to find the $4$-sheet covering of the wedge sum of two circles
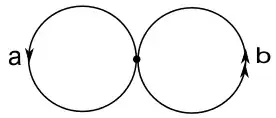
I don't know even how to begin, I know just the definitions of coverings and simple examples, I really need help here.
Thanks a lot
I'm trying to find the $4$-sheet covering of the wedge sum of two circles

I don't know even how to begin, I know just the definitions of coverings and simple examples, I really need help here.
Thanks a lot
It is mentioned in page 61 of Hatcher that the cardinality of the fibre $p^{-1}(x)$ is locally constant (by definition of $p$ being a local homeomorphism) and so if $X$ is connected the cardinality is constant over all of $X$. Now the wedge of two circles is clearly path connected and so we can speak of the number of elements in $p^{-1}(x)$ being the number of sheets of the covering $p : \tilde{X} \to X$.
So for example on page 58, examples 7,8 and 9 are 4 - sheeted covering spaces of $S^1 \vee S^1$. Why is this so? Well look at example 7. Inside of a circle is inscribed a deformed square, and this deformed square meets the circle at 4 points. Those 4 points are indeed the pre - images of the basepoint of $S^1 \vee S^1$ under the covering map that sends an edge labled $b$ in $\tilde{X}$ to the corresponding edge $b$ in $S^1 \vee S^1$ and similarly for $a$. So the cardinality of the fibre is equal to the number of vertices that meet the circle drawn, which is 4.
Finally I should say that when I first learned algebraic topology I found this confusing too, as the definition of a covering map is given but then no explicit proof /map is given for why something is a covering space in most of chapter 1.3. The idea of Hatcher is to give some geometric intuition for this thing and is not meant to be "super - rigorous".
If you want to know how the fundamental group of each of 7,8,9 is calculated, I suggest looking here. Let me know if there is anything more I can add to my answer.