The problem can be modelled through a Markov chain / deterministic finite automaton on four states, $\{T,H,HH,HHT\}$:
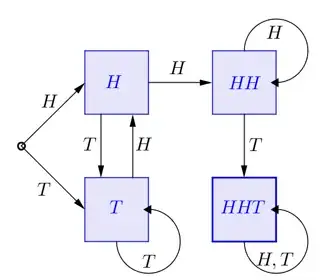
whose transition matrix (assuming the coin is fair) is given by
$$ P=\begin{pmatrix}\frac{1}{2}&\frac{1}{2}&0&0\\\frac{1}{2}&0&\frac{1}{2}&0\\ 0 & 0 & \frac{1}{2} & \frac{1}{2}\\ 0 & 0 & 0 & 1\end{pmatrix} $$
The probability of being in the accepting state $HHT$ after $n$ tosses is given by $$p_n=\left(\tfrac{1}{2},\tfrac{1}{2},0,0\right) P^n \left(0,0,0,1\right)^T = v P^n w^T.$$
The only way to reach $HHT$ is through $HH$. If we assume that $E_{HH}$ is the average number of throws needed to reach $HH$, with probability $\frac{1}{2}$ we go from $HH$ to $HHT$ in a single step, with probability $\frac{1}{4}$ in two steps, with probability $\frac{1}{8}$ in three steps and so on. It follows that
$$ E_{HHT} = E_{HH}+\sum_{n\geq 1}\frac{n}{2^n} = E_{HH}+2.$$
The only way to reach $HH$ is through $H$. The number of strings over the alphabet $\Sigma=\{H,T\}$ with length $n\geq 1$, ending in a $H$ and without consecutive $H$s is given by the Fibonacci number $F_n$. The number of such strings which also starts with an $H$ is given by $F_{n-2}$. It follows that
$$ E_{HH} = E_H + \sum_{n\geq 1}\frac{nF_{n-2}}{2^n} = E_H + 4.$$
Clearly $E_H=2$, hence $E_{HHT} = 2+4+2 = \color{red}{8}$. I leave to you to understand how this number relates to the spectrum of $P$, namely through
$$ E_{HHT} = \sum_{\substack{\lambda\in\text{Spec}(P)\\\lambda\neq 1}}\frac{1}{1-\lambda}.$$
