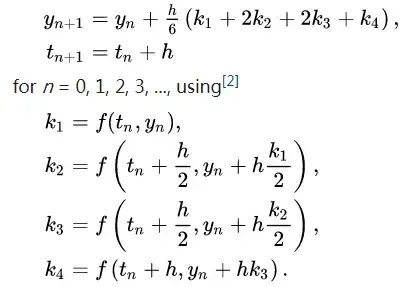In many textbooks, the Runge-Kutta method is introduced for a single 1st order equation
$$ \frac{d y }{dt } = f(t, y ) . $$
It is stated that the method generalizes directly to the multi-component case too, i.e.,
$$ \frac{d \vec{y }}{dt} =\vec{ f} (t, \vec{y }) . $$
Can anyone explain that why this is obvious?
Of course it is not obvious, as there is a 5th order method by Kutta in his original paper (see https://math.stackexchange.com/a/2527316/115115 and the cited paper on the history of RK methods therein) that is correct for scalar ODE but not correct to 5th order for systems. One would need to check the order conditions. Which has been done extensively for the classical RK4 method, so you can use it without problems on systems.
In computing the relevant Taylor expansions of the exact solution and the RK stages and step, there appear terms that are identical for scalar ODE but different for systems where one can not change the order of derivatives. The first is $$ f'[f''[f,f]]\text{ versus } f''[f'[f],f] $$ where $f''[u,v]$ is the second derivative as vector valued symmetric 2-form evaluated in directions $u$ and $v$. In scalar ODE all the derivatives are scalar and both terms equal to $f''f'f^2$, in non-scalar ones they are in general different. This means that for scalar equations these two terms collapse into one conditions, while for systems they establish two different conditions on the coefficients of the RK method.
These terms occur in the order conditions for 5th order, no such ambiguity exists in terms up to 4th order. In other words, up to 4th order what works in the scalar case also works for systems.
