Show that $\sin^2(x)+\sin^2(y)+\sin^2(z) \le9/4$ where $x, y, z$ are angles of a triangle

Question

Let $x, y, z$ are angles of a triangle then $$\sin^2(x)+\sin^2(y)+\sin^2(z) \le \frac{9}{4}.$$

I've tried to use the Jensen's inequality, but it can't help with $\sin^2(x)$...

Answer 1

By multiplying both sides by $4R^2$ we get $a^2+b^2+c^2\leq 9R^2$. This clearly holds since

$$OH^2 = 9R^2-(a^2+b^2+c^2)\geq 0, $$ see this question. A self-contained explanation might proceed as follows:

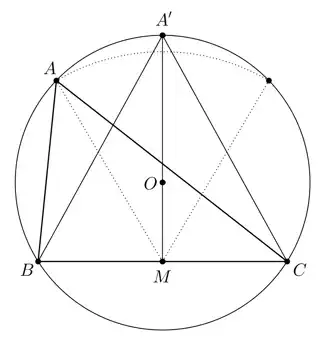
Assume that $A,B,C$ lie on some circle centered at $O$, with $B,C,O$ being fixed and $A$ being free to move on the (major, or minor) $BC$-arc. Let $M$ be the midpoint of $BC$. It is straightforward to notice that $AB^2+AC^2$ only depends on $AM^2$, hence it is maximized when $A$ lies on the perpendicular bisector of $BC$. It also follows that among the triangles with the same circumradius, the equilateral triangles (and they only) maximize the sum of the squared side lengths, so $a^2+b^2+c^2\leq 9R^2$.

Answer 2

By the standard notation we need to prove that $$\sum_{cyc}\frac{4S^2}{b^2c^2}\leq\frac{9}{4}$$ or $$\sum_{cyc}a^2\sum_{cyc}(2a^2b^2-a^4)\leq9a^2b^2c^2$$ or $$\sum_{cyc}(a^6-a^4b^2-a^4c^2+a^2b^2c^2)\geq0,$$ which is Schur.

Done!

I used $$S_{\Delta ABC}=\sqrt{p(p-a)(p-b)(p-c)}=\frac{1}{4}\sqrt{(a+b+c)(a+b-c)(a+c-b)(b+c-a)}=$$ $$=\frac{1}{4}\sqrt{2(a^2b^2+b^2c^2+c^2a^2)-a^4-b^4-c^4},$$ where $p=\frac{a+b+c}{2}.$

Answer 3

If $S=\sin^2A+\sin^2B+\sin^2C$

Using Prove that $\cos (A + B)\cos (A - B) = {\cos ^2}A - {\sin ^2}B$,

$S=1-(\cos^2A-\sin^2B)+1-\cos^2C=2-\cos(A+B)\cos(A-B)-\cos^2C$ $=2+\cos C\cos(A-B)-\cos^2C$

$$\cos^2C-\cos C\cos(A-B)+S-2=0$$

which is a Quadratic Equation in $\cos C$ which is definitely real,

so the discriminant must be $\ge0$

$$\cos^2(A-B)-4(S-2)\ge0\iff4S\le8+\cos^2(A-B)\le8+1$$

The equality occurs if

$\cos^2(A-B)=1\iff\sin(A-B)=0\iff A-B=0$ as $0<A,B<\pi$

$\implies\cos C=\dfrac{\cos(A-B)}2=\dfrac12\implies C=\dfrac\pi3$

and $A=B=\dfrac{A+B}2=\dfrac{\pi-C}2=?$

$\implies A=B=C$