I need to translate the following sentence:
Whenever the alarm sounds the fan must be on and the building empty
into a logical proposition.
So I defined variable as follow:
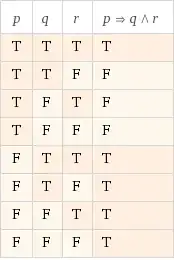
$p$ = "The alarm sounds"
$q$ = "The fan is on"
$r$ = "The building is empty"
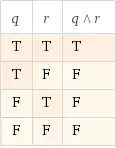
The answer: $p \to (q ∧ r).$
I'm confused by this question because if the alarm does not sound and the fan is not on and the building is not empty then by implication doesn't this mean the statement is true?