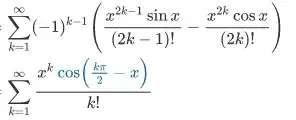1

enter image description here

I was going through a question's solution, where they have used the above identity. I have tried to break my head over how the difference of the two terms got nicely converted to a simple cosine; but I can't seem to understand how the author of the solution did it.

I have tried looking for the Taylor Expansion of cosx in the difference, but in vain.

I also tried to factor out k! from the denominator, but it left me with a messier expression than before. (Of course, it'd be the multiplication of natural numbers from k+1 to 2k-1 or 2k)

Could someone please help me with this algebraic/trigonometric manipulation that the write of the solution has done? A detailed explanation would be great. Thanks.

stoic-santiago
  • 13,705

2 Answers2

1

Note that we can write the expression: $$\cos \left(\frac{k\pi} {2}-x \right) = \cos \frac{k\pi} {2}\cos x - \sin \frac{k\pi} {2} \sin x$$

Now note that:

$$ \sin \frac{k\pi} {2} = \begin{cases} 0 & \text{even k} \\ (-1)^{\frac{k-1}{2}} & \text{odd k} \end{cases} $$

$$\cos \frac{k\pi} {2} = \begin{cases} (-1)^{\frac{k}{2}} & \text{even k} \\ 0 & \text{odd k} \end{cases} $$

Then, it is just a matter of simple arithmetic.

1

$$\sum_{k=1}^\infty\dfrac{x^k\cos\left(\dfrac{\pi k}2-x\right)}{k!}$$

$$=\sum_{r=1}^{\infty}\left(\dfrac{x^{2r-1}\cos\left(\dfrac{\pi(2r-1)}2-x\right)}{(2r-1)!}+\dfrac{x^{2r}\cos\left(\dfrac{\pi(2r)}2-x\right)}{(2r)!}\right)$$

Now,

$k=2r-1\implies\cos\left(\dfrac{\pi k}2-x\right)=\cos\left(\pi r-\dfrac\pi2-x\right)=(-1)^r\cos\left(\dfrac\pi2+x\right)=-(-1)^r\sin x$

Similarly, $k=2r\implies\cos\left(\dfrac{\pi k}2-x\right)=\cdots=(-1)^r\cos x$

lab bhattacharjee
  • 274,582