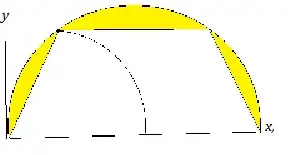
If the second curve has equation $r=2a\cos\theta$, it's a circle.
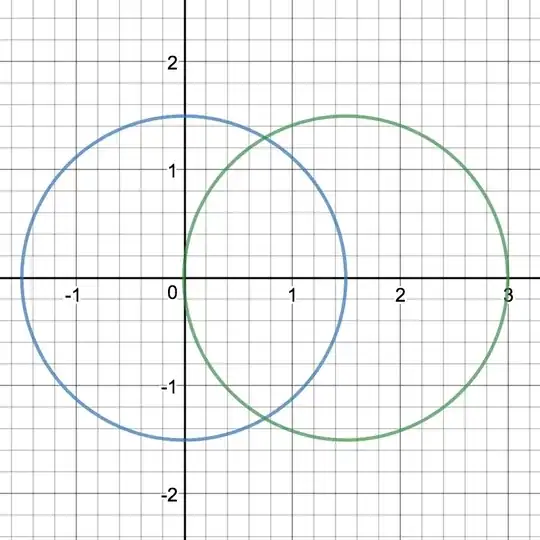The two circles intersect when
$$
2a \cos\theta = a \implies \cos\theta = \frac{1}{2} \implies \theta = \pm\frac{\pi}{3}
$$
Therefore the area of the region is
\begin{align*}
\int_{-\pi/3}^{\pi/3} \int_a^{2 a\cos\theta} r\,dr\,d\theta
&= 2 \int_{0}^{\pi/3} \int_a^{2 a\cos\theta} r\,dr\,d\theta \\
&= \int_{0}^{\pi/3}\left. r^2 \right|_a^{2 a\cos\theta} \,d\theta \\
&= \int_{0}^{\pi/3}\left(4a^2\cos^2\theta - a^2\right)\,d\theta \\
&= a^2 \int_{0}^{\pi/3}\left(2(1+\cos2\theta) - 1\right)\,d\theta \\
&= a^2 \int_{0}^{\pi/3}\left(1+2\cos2\theta\right)\,d\theta \\
&= a^2 \left[\theta+\sin 2\theta\right]_{0}^{\pi/3}\\
&= a^2 \left(\frac{\pi}{3} + \frac{\sqrt{3}}{2}\right)
\end{align*}
If the second curve has equation $r=2a\cos2\theta$, it's a rose of four leaves.
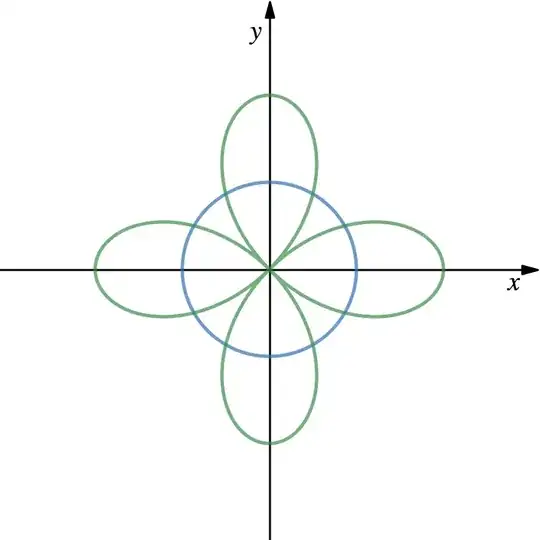The curves intersect when
$$
a = 2a \cos2 \theta \implies \cos2 \theta = \frac{1}{2}
$$
The portion in the right half-plane has three components. Let's find the area of the largest component. That is the portion with $-\frac{\pi}{6} \leq \theta \leq \frac{\pi}{6}$. Its area is
$$
A = 2 \int_0^{\pi/6}\int_0^{2a\cos2 \theta} r\,dr\,d\theta
$$
Substituting $\phi = 2\theta$ and $d\phi = 2d\theta$ transforms this integral into the previous one. So
$$
A = \frac{1}{2}\cdot a^2 \left(\frac{\pi}{3} + \frac{\sqrt{3}}{2}\right)
= a^2 \left(\frac{\pi}{6} + \frac{\sqrt{3}}{4}\right)
$$
