5

I know that the sum of the cubes of the first $n$ natural numbers is
$\{\frac {n(n+1)}2\}^2$ but I am looking for a method to derive this. If there is a method please try to make as simple as possible and possibly without the use of mathematical induction or calculus.

I apologize if I sound ungrateful but I am looking for a way to derive it without using anything to do with Binomial Theorem, Calculus, Mathematical Induction or the fancy notation that almost all answers contain.

If there is no such method then can someone explain what the notation on top of and on the bottom of the Sigma symbol? Like this one $\sum_{i=1}^n$ I do not understand what this means.

I do know how the sum of the first $n$ natural numbers using the Gaussian Method as a derivation, however, I am not sure even about the sum of the first $n^2$ natural numbers.

Prakhar Nagpal
  • 1,312

4 Answers4

7

$$(n+1)^4-1^4=\sum_{i=1}^{n} (i+1)^4-i^4=4\sum_{i=1}^{n}i^3+6\sum_{i=1}^{n}i^2+4\sum_{i=1}^{n}i+\sum_{i=1}^{n}1$$

Assuming you know that: $\sum_{i=1}^{n}i^2=\frac{n(n+1)(2n+1)}{6}$, $\sum_{i=1}^{n}i=\frac{n(n+1)}{2}$, $\sum_{i=1}^{n}1=n$ we can plug this in and solve:

$$4\sum_{i=1}^{n}i^3=(n+1)^4-1-6\left (\frac{n(n+1)(2n+1)}{6}\right )-4\left (\frac{n(n+1)}{2}\right )-n=n^2(n+1)^2$$ And thus $$\sum_{i=1}^{n}i^3=\frac{n^2(n+1)^2}{4}=\left ( \frac{n(n+1)}{2}\right)^2$$

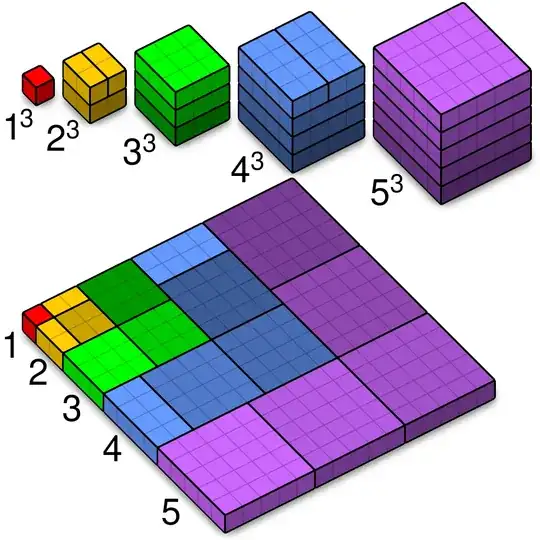Edit: a nice picture from Wikipedia: Notice the pattern between even and odd numbers.

cansomeonehelpmeout
  • 12,782
  • 3
  • 22
  • 49
  • Correct me if I am wrong but isn't the first statement a method used in mathematical induction? – Prakhar Nagpal Jan 10 '18 at 13:50
  • @PrakharNagpal Are you talking about using $\sum_{i=1}^{n}i^2$, $\sum_{i=1}^{n}i$ and $\sum_{i=1}^{n}1$ to find $\sum_{i=1}^{n}i^3$? I agree that the relationship is recursive, but I'm not sure if I would call it proof by induction.

    Induction would be something like: Assume $1^3+2^3+\dots+n^3 = \left (\frac{n(n+1)}{2}\right )^2$

     – cansomeonehelpmeout Jan 10 '18 at 13:59
  • but usually in mathematical induction and again correct me if I am wrong because I have just started studying introduction to mathematical induction on my own don't we prove a certain statement for $n$ and $n+1$ and then say it is true for all values for all values or something of that sort which is what looks like has been done here? Please correct me if I am wrong. – Prakhar Nagpal Jan 10 '18 at 14:04
2

If you already know the sum $S_1$ of the $n$ natural numbers, and the sum $S_2$ of their squares, you can easily derive it:

Start from the binomial formula $\,(k+1)^4=k^4+4k^3+6k^2+4k+1$, which we rewrite as $$(k+1)^4-k^4=4k^3+6k^2+4k+1$$ Summing it for $k=1$ to $n$, we obtain $$(n+1)^4-1^4=4S_3+6S_2+4S_1+n,$$ whence the formula $$S_3=\frac14\bigl((n+1)^4-(n+1)-6S_2-4S_1\bigr).$$

Bernard
  • 175,478
1

You can derive it from the fact that the sum of the first $k$ odd numbers (up to $2k-1$) is $k^2$. That is, $k^2 = \sum_{i=1}^k (2i - 1)$.

We can write $k^3$ = $k\cdot k^2 = \sum_{i=1}^k k^2 = \sum_{i=1}^k k^2 + (\sum_{i=1}^k (2i-1) - k^2) = \sum_{i=1}^k (k^2 - k - 1 +2i) $

This is the sum of all odd numbers from $k^2 - k +1$ through $k^2 + k - 1$.

The next odd number is $k^2 + k + 1 = (k+1)^2 - (k+1) + 1$, i.e., the first odd number contributed by the $(k+1)^3$ term.

Thus the sum of first $n$ cubes is the sum of the odd numbers through $n^2 + n - 1 = 2\frac{n(n+1)}{2} - 1$, which is $\left[\frac{n(n+1)}{2}\right]^2$.

BallBoy
  • 14,472
0

I do not think that this is correct.
$\frac{n(n+1)}{2}=\sum_{i=1}^n i$.

For a dervation on that you can look at it like this:
Let $S=\sum_{i=1}^n i$. Then $2S=\sum_{i=1}^n 2i=n+\sum_{i=1}^n (i+n-i)=n(n+1)$, therefore $S=\frac{n(n+1)}{2}$

Pink Panther
  • 841