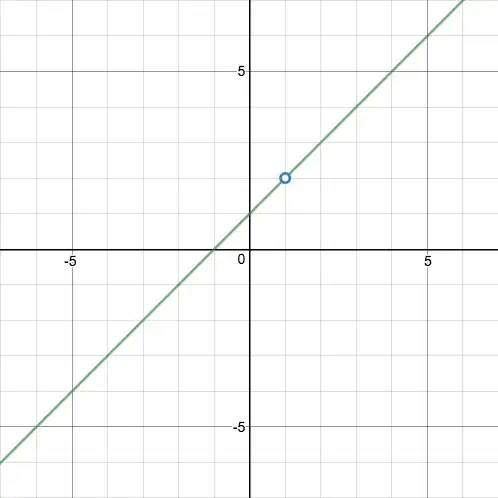
Say I am trying to solve this limit:
$\lim_{x \to 1} \frac{x^2-1}{x-1}$
I know the answer is 2 because:
$\lim_{x \to 1} \frac{x^2-1}{x-1} = $
$\lim_{x \to 1} \frac{(x+1)(x-1)}{x-1} = $
$\lim_{x \to 1} x+1 = $
But on a high level, what is going on here? We can't use direct substitution because at 1, the function is not defined. But why does cancellation help? Why does the common factor cause problems? Why does cancelling the common factor fix our problem (whatever it is)?
Intuitively, $\lim_{x \to 1}f(x)$ means that $x$ is approaching $1$ without letting $x=1$. Because $\frac{(x+1)(x-1)}{x-1}$ is defined for any $x\neq 1$ (so also for $x$ very close to $1$), we have that $\frac{(x-1)}{x-1}=1$.
Now because $\frac{x^2-1}{x-1} =\frac{(x+1)(x-1)}{x-1}$ for $x\neq 1$, this limit is well-defined for $\frac{x^2-1}{x-1}$ too.
So in general $f(x)$ doesn't have to be defined at $a$ to calculate $\lim_{x \to a}f(x)$, but $f(x)$ must be defined near $a$, else you couldn't take a limit anyway.
I don't know if this explanation would help you understand the problem or not, bu it is how i see it. In the given example, it is like you have initially $\lim\limits_{x\to 1}$x+1 and then you multiply it by $\frac{0}{0}$( which is an indefined quantity) in the form of a limit i.e. $\frac{x-1}{x-1}$..
So when you have the compact form $\frac{x^2-1}{x-1}$, you don't see the problem unless you decompose it.
So the main problem in this type of limit calculation is the indetermined form like $$\frac{0}{0},\ 0\cdot \infty,\ +\infty-\infty $$
At every point other than $x=1,$ the function $f(x) = \frac{x^2-1}{x-1}$ (depicted above) looks exactly like the function $g(x) = x+1.$ The limit $\lim_{x\to1} f(x)$ doesn't mean "evaluate $f(1),$" it means "find the value that $f$ gets really close to as $x$ gets really close to 1." As you can see in the picture above, as $x$ approaches 1, $f(x)$ approaches 2.
