3

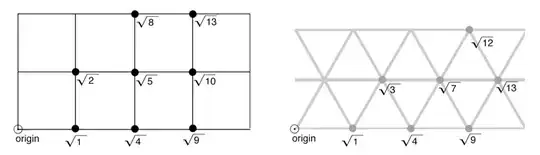
Different Grids

In a standard square grid pattern the distances to integer root locations is simply the sum of two squares. We find that these distances have $\sqrt1, \sqrt2, \sqrt4, \sqrt5, \sqrt8, \sqrt9, \sqrt10, \sqrt13, ...$ But, knowing it's the sum of two squares we know this is Fermat's theorem on the point and that these exist so long as the prime factors of the number are even for $4k + 3$. So $3$ is absent because $3$ has prime factors of $3$ and there's 1 $3$ which is odd and $4*0+3 = 3$. $6$ is missing as it has prime factors $2,3$, which is again an odd number of $3$s. $7$ is also missing as $4*1+3 = 7$ and the prime factors of $7$ are $7, 1$. We also don't have $11$, as $11$ is $4*2+3 = 11$. $12$ is gone because prime factors are $3,2,2$ which is an odd number of 3s.

In this case the root-integer distances are the same as the sum of squares, and so we see the pattern.

See: https://en.wikipedia.org/wiki/Fermat%27s_theorem_on_sums_of_two_squares

Now, to the question: is there a similar pattern for an isometric grid? And if so what? I mean it's missing $\sqrt2, \sqrt5, \sqrt6, \sqrt8, \sqrt10, \sqrt11$ but why?

For further info on the background of the question: http://www.fractalcurves.com/Root6.html

Tatarize
  • 177

1 Answers1

1

The numbers that appear in the square grid are the ones representable by the quadratic form $a^2 + b^2$, whereas the numbers that appear in a hexagonal grid are the ones representable by the quadratic form $a^2 + ab + b^2$. These are classified in a way analogous to the classification of sums of two squares:

A positive integer $n$ can be written in the form $a^2 + ab + b^2$ iff each prime factor of $n$ congruent to $2 \bmod 3$ divides it an even number of times.

This is why the primes congruent to $2 \bmod 3$ like $2, 5, 11$, etc. don't appear. This can be proven in several ways; one is to analyze primes in the Eisenstein integers.

Qiaochu Yuan
  • 419,620