I'm reading a book on Bayesian statistics and I came across the following:
Suppose that $\Psi = g(\Theta)$ and that $f$ is a density function. Then $f_\Psi(\psi) = f_\Theta(g^{-1}(\psi))\bigg|\dfrac{d}{d\psi}g^{-1}(\psi)\bigg|$.
Question: Why is this true? I can't find the appropriate theorem do justify this, and I can't figure it out myself.
Thanks in advance!
You have assumed $g$ is invertible. If $g$ is continuous, that can happen only if $g$ is strictly monotone. So here I will consider the case where $g$ is strictly increasing. In that case $g^{-1}$ is also strictly increasing, so $\dfrac d {d\psi} g^{-1}(\psi)\ge 0$ for all $\psi$ (possibly being equal to $0$ at some isolated points).
We have the c.d.f. $F_\Psi(\psi) = \Pr(\Psi \le \psi),$ and then \begin{align} f_\Psi(\psi) & = \frac d {d\psi} F_\Psi(\psi) = \frac d {d\psi} \Pr( g(\Theta) \le \psi) = \frac d {d\psi} \Pr(\Theta \le g^{-1}(\psi)) = \frac d {d\psi} F_\Theta(g^{-1}(\psi)) \\[10pt] & = f_\Theta(g^{-1}(\psi)) \cdot \frac d {d\psi} g^{-1}(\psi) \quad \text{by the chain rule.} \end{align} The decreasing case is done similarly; some inequalities get inverted.
(Sorry, I realized that you used $\Theta$ at the last minute. Simply replace $X$ with $\Theta$ in my answer below in the context of your question.)
Suppose $\Psi = g(X)$ is (strictly) monotonic with $g^{-1}$ differentiable. Note also that $X$ and $\Psi$ are assumed to be continuous random variables.
We find the density (PDF) of $\Psi$ by finding first the cumulative distribution function (CDF) of $\Phi$ and differentiating the CDF.
Observe $$F_{\Psi}(\psi) = \mathbb{P}(\Psi \leq \psi) = \mathbb{P}(g(X) \leq \psi)\text{.}$$
Case 1. Suppose $g$ is strictly increasing. Then its inverse $g^{-1}$ is also increasing.
Consider the event $\{g(X) \leq \psi\}$.
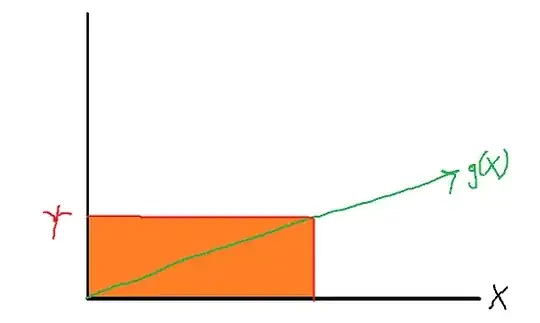
The corresponding values of $X$ such that $g(X) \leq \psi$ are thus those where $X \leq g^{-1}(\psi)$.
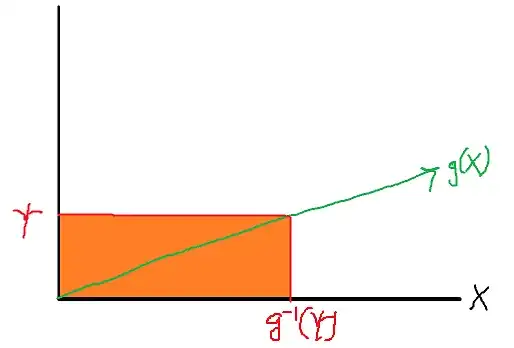
Hence,
$$F_{\Psi}(\psi) = \mathbb{P}(g(X) \leq \psi) = \mathbb{P}(X \leq g^{-1}(\psi)) = F_{X}(g^{-1}(\psi))\text{.}$$ and differentiating (don't forget the chain rule), we obtain: $$F_{\Psi}(\psi) = f_{X}(g^{-1}(\psi))\cdot \dfrac{\text{d}}{\text{d}\psi}g^{-1}(\psi)$$ Since $g^{-1}$ is strictly increasing, it follows that $\dfrac{\text{d}}{\text{d}\psi}g^{-1}(\psi) > 0$, so $\dfrac{\text{d}}{\text{d}\psi}g^{-1}(\psi) = \left|\dfrac{\text{d}}{\text{d}\psi}g^{-1}(\psi)\right|$.
Case 2. Suppose $g$ is strictly decreasing. Then its inverse $g^{-1}$ is also decreasing.
Consider the event $\{g(X) \leq \psi\}$.
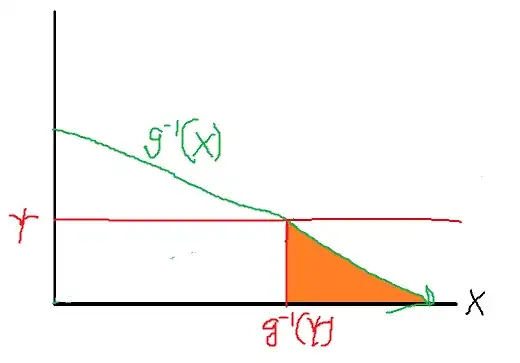
As we can see above, the corresponding values of $X$ such that $g(X) \leq \psi$ are those where $X \geq g^{-1}(\psi)$. Hence,
$$F_{\Psi}(\psi) = \mathbb{P}(X \geq g^{-1}(\psi)) = 1 - F_{X}(g^{-1}(\psi))\text{.}$$ Differentiating and applying the chain rule, we obtain $$f_{\Psi}(\psi) = -f_{X}(g^{-1}(\psi)) \cdot \dfrac{\text{d}}{\text{d}\psi}g^{-1}(\psi)$$ but notice that in this case, $g^{-1}$ is decreasing so $\dfrac{\text{d}}{\text{d}\psi}g^{-1}(\psi) < 0$. Notice the negative coefficient with $f_{\Psi}$. This would this turn $\dfrac{\text{d}}{\text{d}\psi}g^{-1}(\psi)$ into its positive form; hence, we have $$f_{\Psi}(\psi) = f_{X}(g^{-1}(\psi)) \cdot \left|\dfrac{\text{d}}{\text{d}\psi}g^{-1}(\psi)\right|$$ In both cases ($g$ strictly increasing, $g$ strictly decreasing), the above equation is true.
