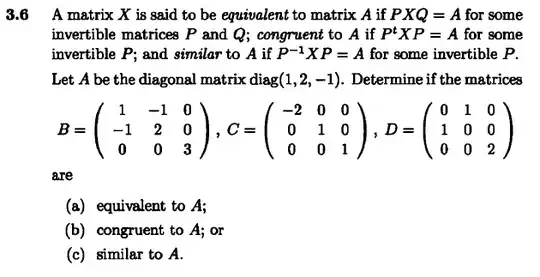ADDED: I'm just answering part (b) about congruence.
Congruence over the real numbers, with real symmetric matrices, is entirely governed by Sylvester's Law of Inertia. Just the signs of the eigenvalues. In turn these may be found without bothering about the eigenvalues themselves. $A$ and $C$ both have eigenvalues in pattern $++-$ and so are congruent over the reals.
However, $B$ has pattern $+++$
$$ E_j^T D_{j-1} E_j = D_j $$
$$ P_{j-1} E_j = P_j $$
$$ E_j^{-1} Q_{j-1} = Q_j $$
$$ P_j Q_j = I $$
$$ P_j^T H P_j = D_j $$
$$ Q_j^T D_j Q_j = H $$
$$ H = \left(
\begin{array}{rrr}
1 & - 1 & 0 \\
- 1 & 2 & 0 \\
0 & 0 & 3 \\
\end{array}
\right)
$$
==============================================
$$ E_{1} = \left(
\begin{array}{rrr}
1 & 1 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1 \\
\end{array}
\right)
$$
$$ P_{1} = \left(
\begin{array}{rrr}
1 & 1 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1 \\
\end{array}
\right)
, \; \; \; Q_{1} = \left(
\begin{array}{rrr}
1 & - 1 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1 \\
\end{array}
\right)
, \; \; \; D_{1} = \left(
\begin{array}{rrr}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 3 \\
\end{array}
\right)
$$
==============================================
$$ P^T H P = D $$
$$\left(
\begin{array}{rrr}
1 & 0 & 0 \\
1 & 1 & 0 \\
0 & 0 & 1 \\
\end{array}
\right)
\left(
\begin{array}{rrr}
1 & - 1 & 0 \\
- 1 & 2 & 0 \\
0 & 0 & 3 \\
\end{array}
\right)
\left(
\begin{array}{rrr}
1 & 1 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1 \\
\end{array}
\right)
= \left(
\begin{array}{rrr}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 3 \\
\end{array}
\right)
$$
$$ Q^T D Q = H $$
$$\left(
\begin{array}{rrr}
1 & 0 & 0 \\
- 1 & 1 & 0 \\
0 & 0 & 1 \\
\end{array}
\right)
\left(
\begin{array}{rrr}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 3 \\
\end{array}
\right)
\left(
\begin{array}{rrr}
1 & - 1 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1 \\
\end{array}
\right)
= \left(
\begin{array}{rrr}
1 & - 1 & 0 \\
- 1 & 2 & 0 \\
0 & 0 & 3 \\
\end{array}
\right)
$$
=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
your $D$ is back to $++-$ I call it $H,$ which stands for Hessian.
$$ E_j^T D_{j-1} E_j = D_j $$
$$ P_{j-1} E_j = P_j $$
$$ E_j^{-1} Q_{j-1} = Q_j $$
$$ P_j Q_j = I $$
$$ P_j^T H P_j = D_j $$
$$ Q_j^T D_j Q_j = H $$
$$ H = \left(
\begin{array}{rrr}
0 & 1 & 0 \\
1 & 0 & 0 \\
0 & 0 & 2 \\
\end{array}
\right)
$$
==============================================
$$ E_{1} = \left(
\begin{array}{rrr}
0 & 0 & 1 \\
0 & 1 & 0 \\
1 & 0 & 0 \\
\end{array}
\right)
$$
$$ P_{1} = \left(
\begin{array}{rrr}
0 & 0 & 1 \\
0 & 1 & 0 \\
1 & 0 & 0 \\
\end{array}
\right)
, \; \; \; Q_{1} = \left(
\begin{array}{rrr}
0 & 0 & 1 \\
0 & 1 & 0 \\
1 & 0 & 0 \\
\end{array}
\right)
, \; \; \; D_{1} = \left(
\begin{array}{rrr}
2 & 0 & 0 \\
0 & 0 & 1 \\
0 & 1 & 0 \\
\end{array}
\right)
$$
==============================================
$$ E_{2} = \left(
\begin{array}{rrr}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 1 & 1 \\
\end{array}
\right)
$$
$$ P_{2} = \left(
\begin{array}{rrr}
0 & 1 & 1 \\
0 & 1 & 0 \\
1 & 0 & 0 \\
\end{array}
\right)
, \; \; \; Q_{2} = \left(
\begin{array}{rrr}
0 & 0 & 1 \\
0 & 1 & 0 \\
1 & - 1 & 0 \\
\end{array}
\right)
, \; \; \; D_{2} = \left(
\begin{array}{rrr}
2 & 0 & 0 \\
0 & 2 & 1 \\
0 & 1 & 0 \\
\end{array}
\right)
$$
==============================================
$$ E_{3} = \left(
\begin{array}{rrr}
1 & 0 & 0 \\
0 & 1 & - \frac{ 1 }{ 2 } \\
0 & 0 & 1 \\
\end{array}
\right)
$$
$$ P_{3} = \left(
\begin{array}{rrr}
0 & 1 & \frac{ 1 }{ 2 } \\
0 & 1 & - \frac{ 1 }{ 2 } \\
1 & 0 & 0 \\
\end{array}
\right)
, \; \; \; Q_{3} = \left(
\begin{array}{rrr}
0 & 0 & 1 \\
\frac{ 1 }{ 2 } & \frac{ 1 }{ 2 } & 0 \\
1 & - 1 & 0 \\
\end{array}
\right)
, \; \; \; D_{3} = \left(
\begin{array}{rrr}
2 & 0 & 0 \\
0 & 2 & 0 \\
0 & 0 & - \frac{ 1 }{ 2 } \\
\end{array}
\right)
$$
==============================================
$$ P^T H P = D $$
$$\left(
\begin{array}{rrr}
0 & 0 & 1 \\
1 & 1 & 0 \\
\frac{ 1 }{ 2 } & - \frac{ 1 }{ 2 } & 0 \\
\end{array}
\right)
\left(
\begin{array}{rrr}
0 & 1 & 0 \\
1 & 0 & 0 \\
0 & 0 & 2 \\
\end{array}
\right)
\left(
\begin{array}{rrr}
0 & 1 & \frac{ 1 }{ 2 } \\
0 & 1 & - \frac{ 1 }{ 2 } \\
1 & 0 & 0 \\
\end{array}
\right)
= \left(
\begin{array}{rrr}
2 & 0 & 0 \\
0 & 2 & 0 \\
0 & 0 & - \frac{ 1 }{ 2 } \\
\end{array}
\right)
$$
$$ Q^T D Q = H $$
$$\left(
\begin{array}{rrr}
0 & \frac{ 1 }{ 2 } & 1 \\
0 & \frac{ 1 }{ 2 } & - 1 \\
1 & 0 & 0 \\
\end{array}
\right)
\left(
\begin{array}{rrr}
2 & 0 & 0 \\
0 & 2 & 0 \\
0 & 0 & - \frac{ 1 }{ 2 } \\
\end{array}
\right)
\left(
\begin{array}{rrr}
0 & 0 & 1 \\
\frac{ 1 }{ 2 } & \frac{ 1 }{ 2 } & 0 \\
1 & - 1 & 0 \\
\end{array}
\right)
= \left(
\begin{array}{rrr}
0 & 1 & 0 \\
1 & 0 & 0 \\
0 & 0 & 2 \\
\end{array}
\right)
$$