Computing an Integral using Contour Integration $\int_0^{\infty} \frac{x^{\alpha}}{x^3 + 1} dx$

Question

How does one compute the integral $\int_0^{\infty} \frac{x^{\alpha}}{x^3 + 1} dx$, where $0 < \alpha < 1$, using contour integration?

Answer 1

Not a proof by contour integration strictly speaking, but a proof through something more versatile, also known as Herglotz' trick.

---

By enforcing the substitution $x=z^{2/3}$ the problem can be solved through the well-known identity

$$ \forall \beta\in(-1,1),\qquad \int_{0}^{+\infty}\frac{z^\beta}{z^2+1}\,dz = \frac{\pi}{2\cos\frac{\pi\beta}{2}}\tag{WNI}$$

Proof: the integral equals $\int_{0}^{1}\frac{x^\beta+x^{-\beta}}{x^2+1}\,dx $ or $$ F(\beta)=\sum_{n\geq 0}(-1)^n\left[\frac{1}{(\beta+2n+1)}+\frac{1}{(-\beta+2n+1)}\right]=\sum_{n\geq 0}\frac{(-1)^n (4n+2)}{(2n+1)^2-\beta^2}$$ which is a meromorphic function with simple poles with residue $\pm 1$ at any odd integer. Since $$\cos\frac{\pi\beta}{2}=\prod_{n\geq 0}\left(1-\frac{\beta^2}{(2n+1)^2}\right) $$ the same holds for $\frac{\pi}{2\cos\frac{\pi\beta}{2}}$. Clearly $F(0)=\frac{\pi}{2}$ and both $F(\beta)$ and $\frac{\pi}{2\cos\frac{\pi\beta}{2}}$ are log-convex functions over the interval $(-1,1)$; the latter by direct inspection, the former through the Cauchy-Schwarz/Holder inequality applied to $ \int_{0}^{+\infty}\frac{z^\beta}{z^2+1}\,dz$. This finishes the proof.

---

By $(\text{WNI})$, for any $\alpha\in(-1,2)$ we have $$ \int_{0}^{+\infty}\frac{x^\alpha}{x^3+1}\,dx = \frac{\pi}{3\cos\frac{\pi(2\alpha-1)}{3}}. $$

Answer 2

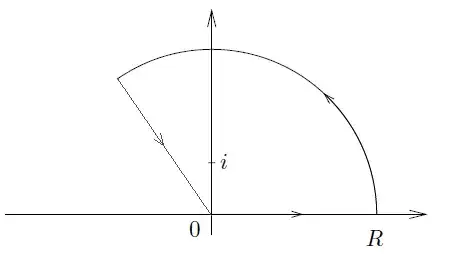
Following Daniel Fischer's advice, namely to use a circular sector of angle $2\pi/3$ with radius $R>1$. The contour is shown below.

Before getting to work, the Logarithm that will be used is the Principal Logarithm. Okay, we integrate the following: \begin{align} \oint_C\frac{z^\alpha}{1+z^3}\,dz \end{align} The only pole inclosed is $z=e^{i\pi/3}$ so we get by the Residue Theorem: \begin{align} \oint_C\frac{z^\alpha}{1+z^3}\,dz&=2\pi i \operatorname{Res}_{z=e^{i\pi/3}}\frac{z^\alpha}{1+z^3}\\ &=2\pi i \frac{e^{i\pi/3}e^{i\alpha\pi/3}}{(e^{i2\pi/3}-e^{-i2\pi/3})(e^{i\pi/3}-e^{-i\pi/3})}\\ &=-i\pi \frac{e^{i\pi/3}e^{i\alpha\pi/3}}{2\sin(\pi/3)\sin(2\pi/3)} \\ &=-i\frac{2\pi}{3}e^{i\pi/3}e^{i\alpha\pi/3} \end{align} Moreover we have: \begin{align} \tag{1} \oint_C\frac{z^\alpha}{1+z^3}\,dz = (1-e^{i\alpha2\pi/3}e^{i2\pi/3})\int^R_0 \frac{t^\alpha}{t^3+1}\,dt + \int_{B_R}\frac{z^\alpha}{1+z^3}\,dz \end{align} The last one is the integral on the circular part and that goes to zero as $R\to\infty$ hence: \begin{align} (1-e^{i\alpha2\pi/3}e^{i2\pi/3})\int^\infty_0 \frac{t^\alpha}{t^3+1}\,dt=-i\frac{2\pi}{3}e^{i\pi/3}e^{i\alpha\pi/3} \end{align} Hence: \begin{align} \int^\infty_0 \frac{t^\alpha}{t^3+1}\,dt&=-i\frac{2\pi}{3}\frac{e^{i\pi/3}e^{i\alpha\pi/3}}{1-e^{i\alpha2\pi/3}e^{i2\pi/3}}\\ \end{align} Simplifying the last expression:

$$\int^\infty_0 \frac{t^\alpha}{t^3+1}\,dt=\frac{\pi}{3\sin[(1+\alpha)\pi/3]}$$

Remark. This answer has almost full elaboration, but there are still things that must be verified, for example $(xy) ^\alpha=x^\alpha y^\alpha$ used in $(1)$ indirectly (does not hold in general).