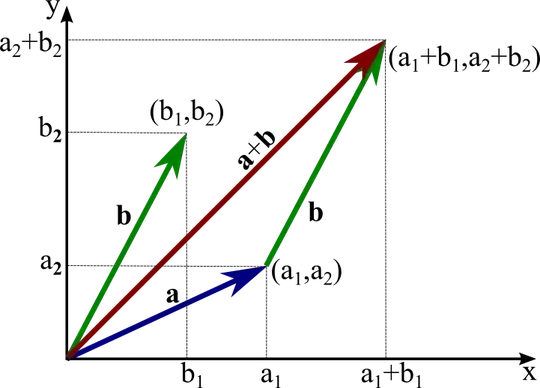
In my book it defines position vectors as vectors that area tied to the origin, ie they can't be moved like free vectors.
Granted that this is a correct definition, it got me thinking: are they even vectors at all? This is because they seem to be the same as coordinates, ie simple points on the plane. After all, coordinates also have a magnitude and a direction, don't they? They are simply not allowed to be moved, that is all. So coordinates and position vectors seem to be the same thing (except when we draw position vectors, we draw the arrow, whereas with coordinates we just draw the point). The fact that we can't move a position vector adds to my doubts regarding why they are called vectors, since they just seem to be points.
Even from the point of view of defining them as vectors because of their algebraic form, ie $x\hat i + y\hat j$, then surely the fact that we can't move them would mean that this is a contradition? Because we are defining a position vector in terms of things that can be moved, ie $\hat i$ and $\hat j$, so it would appear from this definition that $x\hat i+y\hat j$ can also be moved, meaning it isn't a position vector.
What then is a position vector?
I'm probably over thinking this though, so any hints in the right direction would be appreciated.
Edit: tl;dr: Why can't we just use coordinate notation for position vectors and agree to write position vectors and coordinates together. E.g. things like $a+\vec b$ where $a=(5,3)$ and $\vec b$ is a vector.