I am interested in an explicit example of smooth partition of unity and I would greatly appreciate if someone could provide me an example for it. Let $[a, b]$ be an interval. I cover it with $U_i = (x_i - d_i, x_i + d_i)$ with $i=1,2,3$. And I would like to see a smooth partition of unity with these three sets. Any comments/suggestions would be appreciated. Thank you very much.
-
2are you not happy with wikipedia's picture of a partition of unity for the circle? https://en.wikipedia.org/wiki/Partition_of_unity – Calvin Khor Jan 02 '18 at 15:36
-
@CalvinKhor I would really like to see the functions defined! – Johnny T. Jan 02 '18 at 15:45
-
1You can assume that these intervals $U_i$ don't overlap too much in the sense that $U_i$ is not a subset of $\cup_{j\neq i} U_j$. Otherwise you can eliminate one of them by taking constant $0$ function as a partition. In that case you can rearrange them so that we have $U_1, U_2, U_3, U_4,\ldots$ and only consecutive intervals intersect nonempty. With that you can build your partitions from smooth transitions from $0$ to $1$ (https://math.stackexchange.com/questions/328868/how-to-build-a-smooth-transition-function-explicitly) by piecewise glueing. – freakish Jan 02 '18 at 16:09
1 Answers
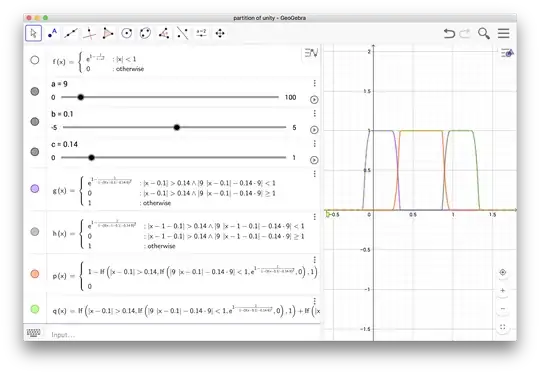
Thrown together in Geogebra. You don't want to touch the b slider, sorry. Parameter a is how steep the bump function needs to be, so that the stuff happening in $U_1$ doesn't interact with the stuff in $U_3$. Parameter c is the size of $U_1\setminus \overline{U_2}$ which I took to also be the size of $U_3\setminus \overline{U_2}$. Allow me to leave what exactly $U_i$ are in this picture as an exercise...
g is your usual bump function that is 1 inside $U_1 \setminus \overline{U_2}$ and quickly drops off to 0 by the time it hits $\partial U_1$.
h is similarly made (actually I was lazy and translated a copy of g).
Once $f_1=$g and $f_3=$h were created, $f_2=$p$=1-g-h$ is easy.
The dashed green line verifies that their sum is 1.
I've done nothing more than roughly follow the construction as laid out in text books, e.g. Lee's Manifolds.
- 34,903