I'm looking for a simple geometrical method of proving that $$\theta < \tan\theta$$ for $0 < \theta < \frac{\pi}{2}$.
I am able to prove that $\sin\theta < \theta$.
Asked
Active
Viewed 670 times
0
-
I presume you mean, "for all $0 < \theta < \frac{\pi}{2}$"? Yours sounds like you are looking for just one $\theta$ where $\theta < \tan \theta$. – Mike Pierce Dec 31 '17 at 17:38
-
I'm curious. How did you prove "geometrically" that $\sin\theta < \theta$? That seems rather odd since $\theta$ is an angle but $\sin\theta$ is a length/measure. – Mike Pierce Dec 31 '17 at 17:42
-
1@MikePierce: θ is not an angle, but a measure of an angle, i.e. the length of an arc on the unit circle (or if you allow negative values, a curvilinear abscissa on the trigonometric circle). – Bernard Dec 31 '17 at 19:42
-
See my related answer here. – dxiv Dec 31 '17 at 21:50
-
Related: https://math.stackexchange.com/questions/2319969/is-the-proof-of-lim-theta-to-0-frac-sin-theta-theta-1-in-some-high-s/2320028#2320028 Lemma. If $A,B$ are convex bounded sets in $\mathbb{R}^2$ and $A\subsetneq B$, the perimeter of $A$ is less than the perimeter of $B$. – Jack D'Aurizio Jan 01 '18 at 13:03
-
1Possible duplicate of Proving $n\sin(\frac{\pi}{n})<\pi<n\tan(\frac{\pi}{n})$ ; obtaining results from it. – Raskolnikov Jan 04 '18 at 19:41
1 Answers
2
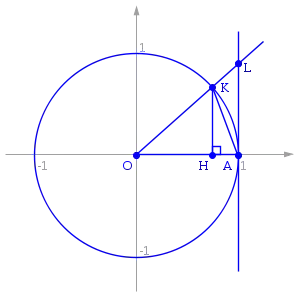$${\displaystyle S_{\triangle OKA}<S_{sectKOA}<S_{\triangle OAL}} \tag1$$
where $ {\displaystyle S_{sectKOA}}$ — area of sector ${\displaystyle KOA} $
$${\displaystyle S_{\triangle KOA}={\frac {1}{2}}\cdot |OA|\cdot |KH|={\frac {1}{2}}\cdot |OA|\cdot |OK|\cdot \sin x={\frac {1}{2}}\cdot 1\cdot 1\cdot \sin x={\frac {\sin x}{2}}}$$ $${\displaystyle S_{sectKOA}={\frac {1}{2}}R^{2}x={\frac {x}{2}}}$$ $${\displaystyle S_{\triangle OAL}={\frac {1}{2}}\cdot |OA|\cdot |LA|={\frac {\mathrm {tan} \,x}{2}}}$$ from $\triangle OAL: |LA|={\mathrm {tan}}\,x$
substitute in $(1)$:
$$ {\frac {\sin x}{2}}<{\frac {x}{2}}<{\frac {{\mathrm {tan}}\,x}{2}}$$
-
1
-
what do you mean? may be "sector"? (https://en.wikipedia.org/wiki/Circular_sector) – aid78 Dec 31 '17 at 17:48
-
Is a sector the region itself, or the area of the region? What is $S_{\triangle\text{stuff}}$? What is $\operatorname{tg}x$? Am I suppose to guess that $R$ is the radius of the circle and $x$ is the angle in question? It's a pain to sift through your notation. – Mike Pierce Dec 31 '17 at 17:53
-
-
-
@Bernard I downvoted. The proof looks correct, but verifying this was very unpleasant. I can't imagine anyone starting to read this answer without feeling a pang of dread at having to parse what's going on. I was hoping aid78 would try to clean up the notation, or add some needed exposition. – Mike Pierce Dec 31 '17 at 20:01
-
It's a sketch. There must remain some effort to do from the the O.P., in my opinion. This is not exactly a do-it-for-me site. – Bernard Dec 31 '17 at 20:06
-
@MikePierce I am ready to explain any questions if it be necessary. I changed all uncorrect tangens names (which you told about). – aid78 Dec 31 '17 at 20:18
-
@Bernard I'm not convinced aid78 intended this to be a sketch. And I'd imagine, of the effort the OP will have to put in towards finishing this problem, most of it will go towards figuring out what aid78 was thinking while writing this solution down. Shouldn't sketches/hints be the other way around? where the OP is given broad ideas and exposition, but the details and the calculations are left to them? – Mike Pierce Dec 31 '17 at 20:24
-
This is the only answer at the moment. It is correct despite the fact the notation is a bit different that the one accepted in the US. The author probably isn't a native English speaker , but willing to help. What's the issue? Never experienced this on other stack exchange sites. – Alexey Jan 01 '18 at 15:28