Proof that $\cos\theta = \sin(\pi/2 +\theta)$

Question

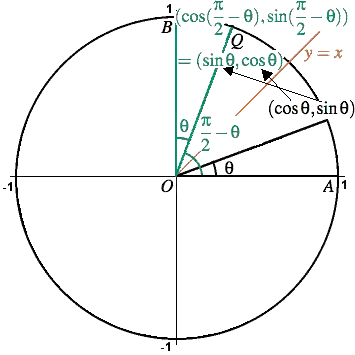
I understand that $\cos(\theta) = \sin(\pi/2 - \theta)$ holds true. But,

Does $\cos(\theta) = \sin(\pi/2 +\theta)$ always hold true?

I am asking this question because I encountered the following question in my workbook.

If $h(x) = \cos x$, $g(x) = \sin x$, and $h(x) = g(f(x))$, which of the following can be $f(x)$?

(a) $-x$

(b) $\pi/2 + x$

(c) $\pi - x$

(d) $3\pi/2 - x$

(e) $3\pi/2 + x$

My book says the correct answer is (b), and I am a bit baffled by this.

I can see that this holds true by plugging in certain values for $x$. But is there a mathematical proof for $\cos(\theta) = \sin(\pi/2 + \theta)$?

See here for a geometric interpretation: https://www.quora.com/Why-does-sin-90+x-equal-cos-x — , Dec 30 '17 at 09:55
Duplicate? "How to remember a particular class of trig identities". In particular, see my answer. — Blue, Dec 30 '17 at 11:02
If you are ok, you can accept the answer and set as solved. Thanks! — user, Dec 31 '17 at 10:31

user · Answer 1 · 2017-12-30T10:00:43.813

3

Yes $$\cos \theta=\sin(\frac{\pi}{2}\pm \theta)$$

always holds.

You can easily prove by trigonometric rules but you can also easily check by graphical observation and symmetry.

You could also prove in this way:

from

$$\cos \theta=\sin(\frac{\pi}{2}- \theta)$$

thus

$$\cos \theta=\cos -\theta=\sin(\frac{\pi}{2}+ \theta)$$

edited Dec 30 '17 at 10:00

answered Dec 30 '17 at 09:53

user

score 3 · Accepted Answer · answered Dec 30 '17 at 09:54

$\sin (\pi/2+x)=\sin (\pi/2)\cos (x)+\cos (\pi/2)\sin (x)=1\times\cos (x)+0\times\sin (x)=\cos (x) $

Or, you can apply what you already know, but to $-x $: $\sin (\pi/2+x)=\sin (\pi/2-(-x))=\cos (-x)=\cos (x) $. ($\cos $ is an "even function".)

2 Answers2