I was going through the following proof:
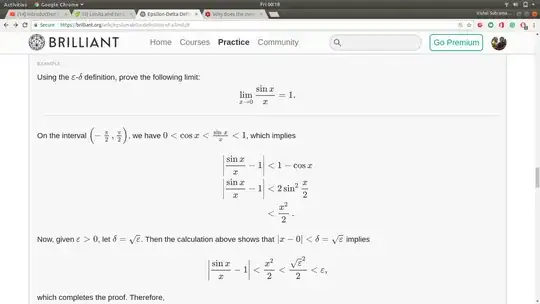
Why is the inequality given in the first line of the proof true? As cos 0 = 1, in the interval (-/2, /2), how can cos x be strictly less than 1?
Why is $cos x < \frac{sin x}{x} $?
I was going through the following proof:

Why is the inequality given in the first line of the proof true? As cos 0 = 1, in the interval (-/2, /2), how can cos x be strictly less than 1?
Why is $cos x < \frac{sin x}{x} $?
The area of the green triangle is $\frac 12 |\sin x|$
The area of the section of the circle (green + red) is $\frac 12 |x|$
And the area of the larger triangle (green + red + blue) is $\frac 12 |\tan x|$
$|\sin x| \le |x| \le |\tan x|$
then with some algebra.
$1 \le \frac {x}{\sin x} \le \sec x\\ \cos x \le \frac {\sin x}{x} \le 1\\ $
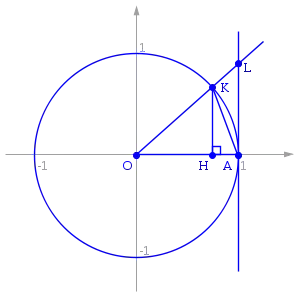 $${\displaystyle S_{\triangle OKA}<S_{sectKOA}<S_{\triangle OAL}} (1)$$
where $ {\displaystyle S_{sectKOA}}$ — square of sector ${\displaystyle KOA} $
$${\displaystyle S_{\triangle OKA}<S_{sectKOA}<S_{\triangle OAL}} (1)$$
where $ {\displaystyle S_{sectKOA}}$ — square of sector ${\displaystyle KOA} $
$${\displaystyle S_{\triangle KOA}={\frac {1}{2}}\cdot |OA|\cdot |KH|={\frac {1}{2}}\cdot |OA|\cdot |OK|\cdot \sin x={\frac {1}{2}}\cdot 1\cdot 1\cdot \sin x={\frac {\sin x}{2}}}$$ $${\displaystyle S_{sectKOA}={\frac {1}{2}}R^{2}x={\frac {x}{2}}}$$ $${\displaystyle S_{\triangle OAL}={\frac {1}{2}}\cdot |OA|\cdot |LA|={\frac {\mathrm {tg} \,x}{2}}}$$ from $\triangle OAL: |LA|={\mathrm {tg}}\,x$
substitute in (1):
$$ {\frac {\sin x}{2}}<{\frac {x}{2}}<{\frac {{\mathrm {tg}}\,x}{2}}$$ for $ x\to 0+:\sin x>0,x>0,{\mathrm {tg}}\,x>0:$
$ {\frac {1}{{\mathrm {tg}}\,x}}<{\frac {1}{x}}<{\frac {1}{\sin x}}$ multiply by $ \sin x$:
$ \cos x<{\frac {\sin x}{x}}<1$
I am afraid that there are all sort of things wrong with the proof you show.
You are right that for $x = 0$ we have $\cos(0) = 1$, so the inequality $$ \cos(x) < 1 $$ certainly does not hold on the interval $\left(\frac{-\pi}{2}, \frac{\pi}{2}\right)$. Even worse, the stated inequality $$ \cos(x) < \frac{\sin(x)}{x} < 1 $$ does not even make sense for $x = 0$, since the middle term is not defined.