Constructing a Regular Pentagon of a Desired Length

Question

I was working on a problem that needed to construct a regular pentagon of a desired length. I couldn’t solve it so checked the solution. The solution in the book was as follows:

1. Draw the line $AB$ of desired length of the pentagon.
2. Draw the perpendicular line $BC$ that is half the original line.
3. Draw hypotenuse $AC$, and extend it as length $BC$ to the point $D$.
4. Draw the circle with radius $BD$.
5. Now, using a ruler, drawing lines that intersect the circle and are the same length as $AB$ will construct a regular pentagon.

I don’t see why this works. And, then again, this solution uses measurements, how can it be done with just a compass and straightedge without measurements.

P.S. I feel bad for not managing to solve this question. How can I improve myself or is this an indicator that I don’t have a good future at math?

Answer 1

This is how to construct a regular pentagon using only a compass and straightedge without measurements.

Answer 2

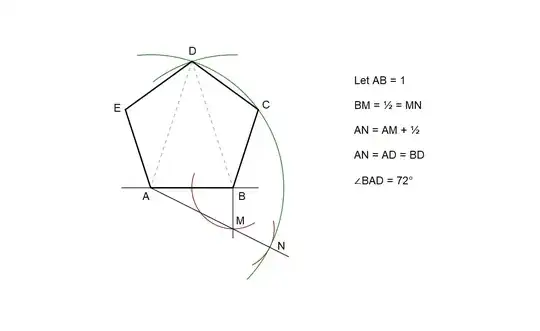
As OP has acknowledged in a comment, the tricky part is Step 4, so we ask

Why is $\overline{BD}$ the desired circumradius?

We can answer this, somewhat unsatisfactorily, using the Law of Cosines on $\triangle ABD$. First, we'll note that the construction gives us these values for an assumed "given" length of $10s$ (to avoid some fractions): $$|\overline{AB}| = 10s \qquad |\overline{AD}| = 5s\left(1+\sqrt{5}\right) \qquad \cos A = \frac{|\overline{AB}|}{|\overline{AC}|}=\frac{2s}{s\sqrt{5}}=\frac{2}{5}\sqrt{5}$$

So, by the Law of Cosines, $$\begin{align} |\overline{BD}|^2 &= (10s)^2 + \left(5s(1+\sqrt{5})\right)^2-2\cdot 10s\cdot 5s(1+\sqrt{5}) \cdot \frac{2}{5}\sqrt{5} \\[2pt] &= 100s^2 + 25s^2 \left( 6 + 2 \sqrt{5} \right)- 40 s^2(\sqrt{5}+5) \\[6pt] &= s^2 \left( 50 + 10 \sqrt{5} \right) \tag{1} \end{align}$$ so that $$|\overline{BD}| = s \sqrt{50 + 10\sqrt{5}} \tag{2}$$

which agrees with MathWorld's for the circumradius of a pentagon with side-length $10s$. $\square$

---

As I mentioned, this answer is unsatisfactory ... which may actually help assuage OP's self-doubts.

Sure, the calculation shows that the numbers work-out how they should, but it sheds no light on how anyone might have expected this result. (I didn't believe it worked until I did the trig verification (twice!), and I'm usually pretty good at perceiving stuff like this. It's what I do.)

More importantly, the calculation gives no indication about how anyone might naturally arrive at the given construction of a pentagon's circumradius. If I were tasked with constructing the length in $(2)$, that construction is not the route I would've taken first ... or even ever. (I probably would've done something far more complicated using the geometric mean construction.)

If, instead, I were asked to construct the pentagon with a given side, it would not have occurred to me to construct that complicated circumradius at all. Rather, I would have gone in the direction of @Seyed's construction, because I "know" the ratio of the diagonal to the side is the Golden Ratio, $(1+\sqrt{5})/2$, and I "know" how to construct a diagonal of the appropriate length. (That's the "obvious" stuff in Steps 1 through 3 of the construction in the question.)

In short: I find the construction in question quite non-intuitive. OP should not feel bad about not understanding the key relation. To be clear:

This IS NOT an indicator that you don't have a good future in math.

(This may be an indicator, though, that whoever devised that surprising construction does (did?) have a good future in math!)