2

I have the following set of 4 Cartesian coordinates:

coords = [3.64811 7.61531 9.05108; 3.53604 4.82801 9.05108; 3.53604 4.82801 6.34192; 3.64811 7.61531 6.34192]

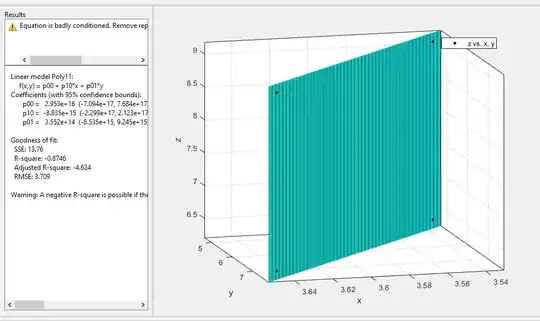
I am trying to fit a plane of the form $ax+by+c=z$ to these 4 coordinates. I tried both the analytical least-squares solution, as described here, and an iterative approach described here. These both result in relatively high root-mean-square-errors but I am not sure why. Using the curve fitting toolbox in MATLAB results in an $r^2$ that's negative and notes that the equation is badly conditioned, although visually the resulting fit looks okay somehow (image below).

It is rather intuitive what the plane should be. What can I do to get a more accurate solution? Mathematically, what is the issue with this set of coordinates?

enter image description here

Argon
  • 183
  • 1
    In general, four points in $\mathbb{R}^3$ don't have to be coplanar.

    However, in your case, there does in fact exist a plane that contains all four points (additionally, your four points are the vertices of a rectangle that is not a square, but this is not directly relevant).

     – Zubin Mukerjee Dec 23 '17 at 04:55
  • Of course, that makes sense. I'm mainly confused because in this case, as you correctly mentioned, the four points are the vertices of a rectangle, so there should be not only a good planar fit but a perfect fit. – Argon Dec 23 '17 at 04:58
  • Can you show the MATLAB code you used to get the least squares fit? – JimmyK4542 Dec 23 '17 at 04:59
  • The above figure was done using the GUI, so I don't have the code for that (I did the rest in Python). But something like the following should replicate it: pinv(A'*A)*A'*B to get a column vector with $a$, $b$, and $c$, where A = horzcat(coords(:,1),coords(:,2),ones(4,1)) and B=coords(:,3) – Argon Dec 23 '17 at 05:05

1 Answers1

1

The problem is that the four points lie on a plane that is vertical. i.e. you can write it as

$$2.78730x-0.11207y-9.3149292113 = 0.$$

So you won't be able to fit a plane of the form $$ax+by+c=z$$ to these points.

JimmyK4542
  • 54,331
  • My end goal is to get the unit normal to the plane that would go through the points. What would be the best way to do so in this circumstance? – Argon Dec 23 '17 at 05:20
  • If a plane can be written in the form $ax+by+cz=d$, then the vector $(a,b,c)$ is normal to the plane. Alternatively, you can take the cross product of two vectors in the plane which aren't parallel or anti-parallel. – JimmyK4542 Dec 23 '17 at 05:22
  • Oh, of course. Yes. That's simple enough. Thank you for your insight. – Argon Dec 23 '17 at 05:25