Homology groups of a Pokeball

Question

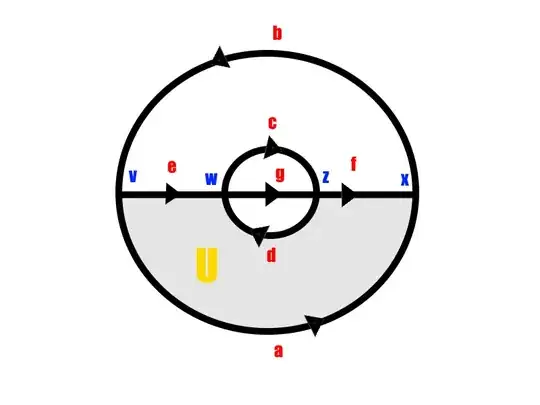
I tried to discover the singular homology groups of a simplex, but I found some dificulties and want to know if someone knows what I've got wrong. The simplex is the following (0-cells are in blue, 1-cells in red and 2-cells in yellow):

As it looks like a Pokeball, I called this space $PB$. First, I drew the following chain complex:

$0\overset{\partial_3}{\rightarrow}\mathbb{Z}\overset{\partial_2}{\rightarrow}\mathbb{Z}^7\overset{\partial_1}{\rightarrow}\mathbb{Z}^4\overset{\partial_0}{\rightarrow}0$

as there are one 2-cell, seven 1-cells and four 0-cells. After it, I concluded the following about the boundary operator $\partial_1$:

$\partial_1 (a)=x-v=\partial^{-1}_1(b)$

$\partial_1(d)=w-z=\partial^{-1}_1(c)=\partial^{-1}_1(g)$

$\partial_1(e)=w-v$

$\partial_1(f)=x-z$

As a clear consequence, $H_0(PB)=\frac{ker\partial_0}{im\partial_1}=\frac{\mathbb{Z}^4}{\mathbb{Z}^4}=0$. As well, we have

$\partial_1(ab)=0$

$\partial_1(cd)=0$

$\partial_1(dg)=0$

$\partial_1(cg^{-1})=0$

After it, I tried to analyse the boundary operator $\partial_2$. Here, however, I found some dificulties. First, how to even define $U$? Would it be equal to $[vwzx]$? I tried to calculate it as if $U=[vwzxv]$, which gave me:

$\partial_2(U)=\partial_2([vwzxv])=-d+a+f+e=e-d+f+a$

which sounded somehow correct to me. However, after it, how could I even compute the kernel of $\partial_2$? Maybe I'm wrong in some definition or I'm using improper concepts. Boundary operators of 2-cells became a huge problem on many of my computations. Thank you for all your answers.

Answer 1

First of all, you have an error in your computation of $H_0$: The image of $\partial_1$ isn't all of $\mathbb Z^4$; it is only the elements where the sum of the coefficients is zero. Note that this is true of the image of every one-simplex, thus of the entire image. In general, $H_0$ contains a copy of $\mathbb Z$ for every path-connected component of the space. Here, thus $H_0(PB)\cong \mathbb Z$

To figure out the boundary of a $2$-cell, you just traverse the boundary clockwise*, and count how many times you cross each edge, plus one if the edge is oriented clockwise and minus one if it is oriented the other ways. So, in this case, you get $f-a+e-d$. (I think you might be confused on definitions here - it looks like maybe you're trying to treat PB as if it were a simplicial complex - which it is not unless you subdivide the square $U$ into two triangles. You need to treat it as a CW-complex if you include a square)

(*It doesn't really matter which way you go, if there are no $3$-cells; if there are cells of higher dimension, you just have to be consistent about how each cell is oriented)

---

To compute $H_1$, you note that the image of $\partial_2$ is just multiples of $f-a+e-d$. The kernel of $\partial_1$ is a bit trickier to deal with, but note that this is just sums that have equally many incoming and outgoing edges to each vertex; that is, we get four equations: $$b-e-a=0$$ $$e+d-g-c=0$$ $$c+g-d-f=0$$ $$f+a-b=0$$ You can check that, for any choice of $(a,b,c,d)\in\mathbb Z^4$, there is exactly one element of $(a,b,c,d,e,f,g)\in \mathbb Z^7$ which satisfies all of these equations. Additionally, one can find that there actually is a basis for $\ker \partial_1$ containing $f-a+e-d$ (since this element is "primitive", meaning it is not a non-trivial multiple of any other element of $\mathbb Z^7$ - or, equivalently, that the GCD of its coefficients is $1$), you see that $H_1(PB)\cong \mathbb Z^3$, since it is $\mathbb Z^4$ mod one the copy of $\mathbb Z$ generated by one of its basis elements.

Then, note that $H_2$ is trivial, since $\partial_2$ has trivial kernel.

---

You might also note that your space is homotopy equivalent to a wedge of three circles, since you can collapse the region $U$ onto the edges $e$ and $d$ and $f$ by a deformation retract. This geometric reasoning makes computing the homology groups way easier.

---

In general, the way you compute the boundary of an $n$-cell $A$ in a CW-complex $X$ is to consider that it's boundary is identified with $S^{n-1}$. For any $(n-1)$-cell $B$, we can consider a quotient map $q:X\rightarrow X/(X\setminus \operatorname{int}(B))$ - that is, the map collapsing everything outside of $Y$ to a point - which is also identified with $S^{n-1}$. Then, you get a map $S^{n-1}\rightarrow S^{n-1}$ by composing the inclusion of the boundary of $A$ into $X$ with the quotient $q$. The degree of this map tells you the coefficient of $B$ in $\partial_n(A)$. In two dimensions, this is basically the definition I gave earlier, but in higher dimensions, it clarifies what is meant by "orientation".