I'm trying to wrap my head around trigonometry. Working in degrees we get:
$$\cos(0°) = 1$$
$$\cos(90°) = 0$$
Half way between $0$ and $90$ degrees we get $45$ degrees, so it seems logical to me that $\cos(45°)$ would give $0.5$, but instead we get $\frac{\sqrt{2}}{2} \simeq 0.7071$, why is that?
The function $f(x) = \cos(x)$ , $f : \mathbb R \to \mathbb R$ is not a linear function, so that assumption that you made will not hold. Note that the value $0.7071$ is not far away from $0.5$ because of the curved line that the $\cos$ function follows on the cartesian coordinate system, which isn't widely deviated from the line $y=x$. This does not mean that other non-linear functions will have "middle-point" values close to $0.5$ (that entirely depends on their polynomial approximation).
Check a simple graph down below :
Also checking the series representation of the cosine $\cos$ function, one can see that is clear that :
$$\cos(x) = \sum_{n=0}^\infty \frac{(-1)^n x^{2n}}{(2n)!}$$
has non-linear terms.
That kind of linear intrapolation requires that you are dealing with a linear function, but you're not. That is, your reasoning would work if the function looked like a triangular see-saw:
But the cosine function doesn't look like that ... see Rebellos' post! (we make a good team!)
For right-angled triangles, where one of the angles is $x\neq90^{\circ}$, I'm sure you know that $\cos x$ is the adjacent side length divided by the length of the hypotenuse.
A right-angled triangle with angle $45^{\circ}$ has opposite and adjacent sides equal in length, so by Pythagoras's Theorem, the hypotenuse is $\sqrt{2}$ times the length of the adjacent side. It follows that $\cos 45^{\circ}=1/\sqrt{2}$.
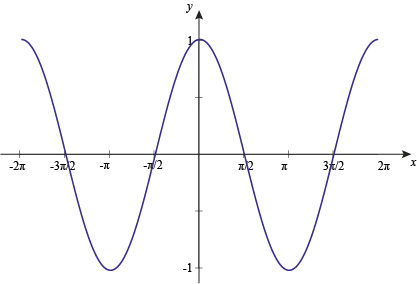
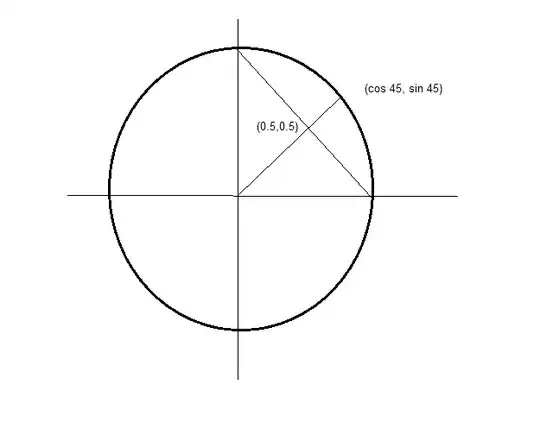
$$ X \in [0°,90°] $$ Are just the inputs to the function $$ f(\color{red}{x}) = \cos(\color{red}{x}), \ x \in X $$.
And $ 45° $ is the mid point of the input, Why it should be necessary that the output is also the mid point?
Consider $$ f(x) = \frac{1}{x} $$ Start inputting $ x= {{ 1,2,3,4,5,6,7,8,9}}$
Here also, $$ f(\color{green}{1}) = \color{green}{1} $$ Now, mid point of input is $5$. But $$ f(\color{green}{5}) = \frac{1}{\color{green}{5}}≠5 $$
Take a look to the trigonometric circle, for an angle of 45 degrees $cos\theta$ is the side of a square with diagonal with length equal to 1 thus it’s equal to $\frac{\sqrt{2}}{2}$.
To better visualize take a look to the following figure:
If you consider a square triangle with angles 90, 45, 45, it is obvious by symmetry that the adjacent and opposite sides are equal; assume they are $1$.
By the pythagorean theorem, the hypotenuse is $h=\sqrt {1^2+1^2}=\sqrt2$. Then $h\,\cos45=1$, so $$\cos45=\frac1h=\frac1 {\sqrt2}. $$
The function $f(x)=x^2$ satisfies $f(0)=1, f(1)=1$, and half way between it is $1/\sqrt{2}$, and maybe that's why $\cos$ is also $1/\sqrt{2}$ half way between.
