Derivation of gradient of SVM loss

Question

Here is the loss function for SVM:

I can't understand how the gradient w.r.t w(y(i)) is:

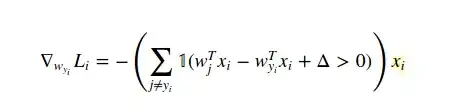
Can anyone provide the derivation?

Thanks

Answer 1

Let's start with basics. The so-called gradient is just the ordinary derivative, that is, slope. For example, slope of the linear function $y=kx+b$ equals $k$, so its gradient w.r.t. $x$ equals $k$. If $x$ and $k$ are not numbers, but vectors, then the gradient is also a vector.

Another piece of good news is that gradient is a linear operator. It means, you can add functions and multiply by constants before or after differentiation, it doesn't make any difference

Now take the definition of SVM loss function for a single $i$-th observation. It is

$\mathrm{loss} = \mathrm{max}(0, \mathrm{something} - w_y*x)$

where $\mathrm{something}=wx+\Delta$. Thus, loss equals $\mathrm{something}-w_y*x$, if the latter is non-negative, and $0$ otherwise.

In the first (non-negative) case the loss $\mathrm{something}-w_y*x$ is linear in $w_y$, so the gradient is just the slope of this function of $w_y$, that is , $-x$.

In the second (negative) case the loss $0$ is constant, so its derivative is also $0$.

To write all this cases in one equation, we invent a function (it is called indicator) $I(x)$, which equals $1$ if $x$ is true, and $0$ otherwise. With this function, we can write

$\mathrm{derivative} = I(\mathrm{something} - w_y*x > 0) * (-x)$

If $\mathrm{something} - w_y*x > 0$, the first multiplier equals 1, and gradient equals $x$. Otherwise, the first multiplier equals 0, and gradient as well. So I just rewrote the two cases in a single line.

Now let's turn from a single $i$-th observation to the whole loss. The loss is sum of individual losses. Thus, because differentiation is linear, the gradient of a sum equals sum of gradients, so we can write

$\text{total derivative} = \sum(I(something - w_y*x_i > 0) * (-x_i))$

Now, move the $-$ multiplier from $x_i$ to the beginning of the formula, and you will get your expression.

Answer 2

David has provided good answer. But I would point out that the sum() in David's answer:

total_derivative = sum(I(something - w_y*x[i] > 0) * (-x[i]))

is different from the one in the original Nikhil's question:

$$ \def\w{{\mathbf w}} \nabla_{\w_{y_i}} L_i=-\left[\sum_{j\ne y_i} \mathbf{I}( \w_j^T x_i - \w_{y_i}^T x_i + \Delta >0) \right] x_i $$ The above equation is still the gradient due to the i-th observation, but for the weight of the ground truth class, i.e. $w_{y_i}$. There is the summation $\sum_{j \ne y_i}$, because $w_{y_i}$ is in every term of the SVM loss $L_i$:

$$ \def\w{{\mathbf w}} L_i = \sum_{j \ne y_i} \max (0, \w_j^T x_i - \w_{y_i}^T x_i + \Delta) $$ For every non-zero term, i.e. $w^T_j x_i - w^T_{y_i} x_i + \Delta > 0$, you would obtain the gradient $-x_i$. In total, the gradient $\nabla_{w_{y_i}} L_i$ is $numOfNonZeroTerm \times (- x_i)$, same as the equation above.

Gradients of individual observations $\nabla L_i$ (computed above) are then averaged to obtain the gradient of the batch of observations $\nabla L$.

Answer 3

In the two answers, I understand that the derivative is only w.r.t $w_{y_i}$ (for only correct score class), additionally, I think that we must derive loss w.r.t $w_{j \neq y_t}$ too, because the gradient $w$ is also connected to other scores. Therefore

$$ \def\w{{\mathbf w}} \nabla_{\w_{j\neq y_i}} L_i=\left[\sum_{j\ne y_i} \mathbf{I}( \w_j^T x_i - \w_{y_i}^T x_i + \Delta >0) \right] x_i $$