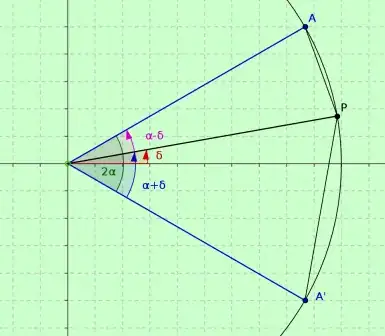
A pentagon is inscribed inside a circle. Prove that the area of the pentagon to be maximum, it must be a regular one.
I have read When is the area of a pentagon inscribed inside a fixed circle maximum?, but am not satisfied with the answer...
My approach:
We can divide the pentagon into a triangle and a cyclic quadrilateral by joining any two vertices. Now we can fix this chord and argue on the maximization of the areas of these two figures...but are we allowed to fix that chord?