Is it possible to draw a Venn diagram with rectangles for $n > 3$? If yes, is it possible for all $n\in\mathbb{N}$? If no, up to which $n$ is it possible?
Furthermore, the rectangles should have the following properties
Solving the given problem I tried different approaches, obtaining better and better bounds. Also the last bound is the best, I leave the other too, because they can help to solve similar problems.
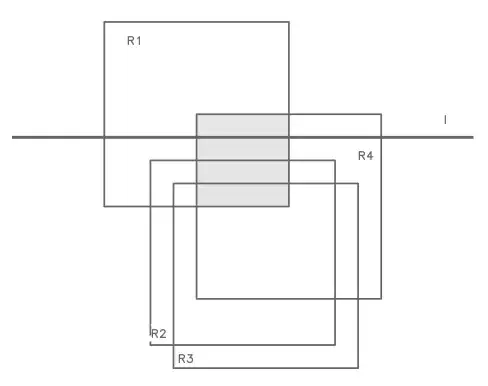
Bound 4. I claim that $n\le 3$. Indeed, assume to the contrary, there exists a family $\mathcal R$ of $4$ (congruent) rectangles representing Venn diagram. Define two orders $\le_x$ and $\le_y$ on $\mathcal R$. Namely, for rectangles $R,R’\in\mathcal R$ put $R\le_t R’$ if $t$-coordinate of the left side of the rectangle $R$ in not bigger that $t$-coordinate of the left side of the rectangle $R’$. Let $R_1\le_x R_2\le_x R_3\le_x R_4$ be the enumeration of the family $\mathcal R$.
Assume first that $R_1$ or $R_4$ is a minimal or a maximal element of $(\mathcal R,\le_y)$. Applying, if needed, to the plane transformations $x\mapsto -x$ and $y\mapsto -y$, without loss of generality we may suppose that $R_1$ is a minimal element of $(\mathcal R,\le_y)$. If $R_2\le_y R_4$ then $R_1\cap R_4\subset R_2$, contradicting the property of Venn diagram. If $R_3\le_y R_4$ then $R_1\cap R_4\subset R_3$, contradicting the property of Venn diagram. Thus $R_4\le_y R_2$ and $R_4\le_y R_3$. Now if $R_2\le_y R_3$ then $R_1\cap R_3\subset R_2$, contradicting the property of Venn diagram and if $R_3\le_y R_2$ then $R_2\cap R_4\subset R_3$, contradicting the property of Venn diagram.
Thus in the order $\le_y$ the elements $R_1$ and $R_4$ are placed between elements $R_2$ and $R_3$. But then $R_1\cap R_4\subset R_2\cup R_3$, contradicting the property of Venn diagram. Indeed, assume to contrary that there is an (interior) point $R_1\cap R_4\setminus (R_2\cup R_3)$. Let $\ell$ be a horizontal straight line going through the point $x$. It is easy to see that if $\ell$ intersects any of rectangles $R_2$ or $R_3$ then it contradicts the choice of $R_1$ or $R_4$ as a leftmost or a rightmost rectangle. Since $R_2$ and $R_3$ intersects, both $R_2$ and $R_3$ lie above $\ell$ or both $R_2$ and $R_3$ lie below $\ell$, a contradiction with that $R_2$ and $R_3$ are topmost and bottommost rectangles.
Bound 3. I claim that $n\le 4$. Indeed, assume to the contrary, there exists a family $\mathcal R$ of $n\ge 5$ (congruent) rectangles representing Venn diagram. Define two orders $\le_x$ and $\le_y$ on $\mathcal R$. Namely, for rectangles $R,R’\in\mathcal R$ put $R\le_t R’$ if $t$-coordinate of the left side of the rectangle $R$ in not bigger that $t$-coordinate of the left side of the rectangle $R’$. By Erdős–Szekeres theorem there exist distinct rectangles $R,R’,R’’\in\mathcal R$ such that $R\le_x R’\le_x R’’$ and either $R\le_y R’\le_y R’’$ or $R’’\le_y R’\le_y R$. Anyway, $R\cap R’’\subset R’$, contradicting the property of Venn diagram.
Bound 2. A more tight upper bound for $n$ can be obtained as follows. Given a partition of the plane into domains by rectangles, consider corners of these domains as vertices of a graph $G$ and the segments of sides of rectangles connecting some of the corners as vertices of the graph. Then each of rectangles of the family contributes at most $4$ its corners to the total number $c$ of the corners, and each two different rectangles of the family additionally contribute to this number at most $4$ in the general case and at most $2$ in your case. Thus $c\le 4n+2n(n-1)=2n^2+2n$ in the general case and $c\le 4n+n(n-1)=n^2+3n$ vertices in your case.
Now double count a number $N$ of pairs $(e, f)$ where $e$ is a edge of the graph $G$ incident to its face $f$. Since, by the construction, each face $f$ of the graph $G$ has degree at least $4$, it contributes at least $4$ to the sum for $N$, implying $N\ge 4r$, where $r$ is the number of faces of the graph $G$, equal to the number of domains in which the rectangles partition the plane. On the other hand, each edge $e$ of $G$ is incident to exactly $2$ faces (we also count the outer face, if needed), so it contributes exactly $2$ to the sum for $N$, implying $N=2m$, where $m$ is the number of edges of the graph $G$. Thus $2m=N\ge 4r$.
Combining the obtained inequality with Euler’s formula $c-m+r=2$, we obtain $r=2+m-c\le m/2$, or $m+4\le 2c$. Then $r=2+m-c\le 2c-2-c=c-2$, which is at most $2n^2+2n-2$ in the general case and at most $n^2+3n-2$ in your case. The inequality $r\ge 2^n$ implies $n\le 6$ in the general case and $n\le 5$ in your case.
Bound 1. Even in a general case, when we do not require that the rectangles has the same width and height, the family consisting of $n$ rectangles span by their sizes at most $2n$ lines parallel to each of the coordinate axis. So they can partition the plane into at most $(2n+1)^2$ domains, whereas Venn’s diagram has $2^n$ domains. So $(2n+1)^2\ge 2^n$, which yields $n\le 8$.
Suppose you have a Venn diagram with $n$ axis-aligned rectangles of the same width and height. By a scaling of the axes, we may assume the rectangles are all squares. Let's show that it's not possible to have a Venn diagram with $n$ axis-aligned squares for $n\ge4$, even if the squares are allowed to be of different sizes.
Suppose there were such a Venn diagram. By shrinking squares as necessary, we can assume the diagram is simple -- that is, each point of intersection of the perimeters of the squares is an intersection of just two squares. In that case, each pair of squares intersects exactly twice, for a total of $2{n\choose2}=n(n-1)$ vertices for the diagram, which implies a total of $2n(n-1)$ (topological) edges. From Euler's formula, $V-E+F=2$, we have
$$F=2+n(n-1)$$
and it's elementary to show that $2^n\gt2+n(n-1)$ for $n\ge4$.
Remark: Because each region in a Venn diagram is an intersection of interiors, the shrinking step(s) can clearly be engineered to leave an open set for each of the $2^n$ intersections, but it's conceivable you could wind up with duplicates of some of the intersections --i.e., the diagram may no longer be a Venn diagram. However, that doesn't matter for the argument here, since it simply says $F\ge2^n$.
Additional remark: The scaling was done for convenience, since it's clear that overlapping squares cannot intersect at more than two points (if the intersections are simple). This is also true for rectangles with a common aspect ratio. It's not true, of course, in general: a tall skinny rectangle can intersect a short fat one at $4$ points as easily as $2$.
