$0$ is marked for the fixed point.
$1$ is marked for the point when you rotate the circle by $1$ radian about its center.
...
When you rotate the circle by $7$ radians, the new marked point is looked like in the picture below:
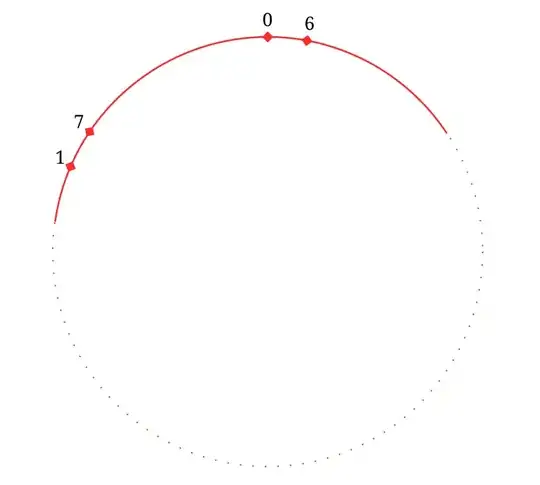
Here is my attempt to solve the problem:
If we straighten out the circle, then all marked points belong to interval $\left[0,2\pi\right)$. Let the set of all marked points is $M$.
Also, if $p_{n}$ is a marked point, created by rotating the fixed point $0$ by $n$ radians, then $p_{n}=n-k2\pi$, where $n,k\in\mathbb{Z}$, and $0\leq p_{n}<2\pi$.
(by observation I think all points of $M$ are the limit points of the set, now try to prove it)
Let $p_{n}\in M$ and suppose the there exists $\varepsilon>0$, that no other than $p_{n}$ belongs to interval $\left(p_{n}-\varepsilon,p_{n}+\varepsilon\right)$, that is $p_{n}$ is an isolated point. This means the point $p_{n+1}$ is also an isolated point, indeed, if there exists $q_{t}\in\left(p_{n+1}-\varepsilon,p_{n+1}+\varepsilon\right)\cap M, q_{t}\neq p_{n+1}$, by rotating “backward” the whole segment $\left(p_{n+1}-\varepsilon,p_{n+1}+\varepsilon\right)$ by 1 radian (rotates by $-1$ radian), we have segment $\left(p_{n}-\varepsilon,p_{n}+\varepsilon\right)$ which contains the point $q_{t-1}\in M$, which contradicts our hypothesis. By induction we could prove that there are infinite isolated point of $M$.
Also, if for $m\neq n, m,n\in\mathbb{N}$, and $p_{n}=p_{m}\Rightarrow m-n=\left(i-k\right)2\pi\Rightarrow\pi=\dfrac{m-n}{2\left(i-k\right)}$. But, $\pi$ is an irrational number, implies that $p_{m}\neq p_{n}$ for all $m,n\in\mathbb{N},m\neq n$.
So, there are infinitely number of intervals which have the form $\left(p_{n}-\varepsilon,p_{n}+\varepsilon\right)$, where $\left|p_{m}-p_{n}\right|\geq\varepsilon$ (if not, $p_{n}\in\left(p_{m}-\varepsilon,p_{m}+\varepsilon\right)$. The length of all of those intervals is infinity when $n\rightarrow\infty$, but the length of $\left[0,2\pi\right)$ is finite.
So, there does not exist isolated point of $M$.
