0

According to Logarithmic exponent rules: log(x^y) = y ∙ log(x)

For example: 2 log x = log x^2

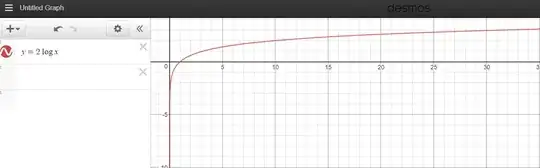
However take the following graphs:

y=2logx enter image description here

y=logx^2 enter image description here

The graphs seems to display something that should not be the case, what am I missing or misunderstanding? I am quite confused.

Sphygmomanometer
  • 231
  • hint: try the graph of $2\log |x|$... – zwim Dec 12 '17 at 01:19
  • 1
    That's because $\log x^2$ is defined for $x\ne$, whereas $2\log x$ is defined for $x>0$. – Bernard Dec 12 '17 at 01:19
  • Got it, I inputted y=logx^2 {x>0} and received the same as y=2logx. – Sphygmomanometer Dec 12 '17 at 01:32
  • I don't think referencing the question "Question about bilinear form on Hilbert space" as saying this is already answered is helpful because if like me you're asking this question, you need a very long explanation to understand how "Question about bilinear form on Hilbert space" is even the same question... – dllahr Mar 24 '21 at 00:53

3 Answers3

1

The domain of $\log x$ and $\log x^2$ is different in the sense that you can plug in negative numbers into $\log x^2$ but not $2\log x$

Teh Rod
  • 3,108
1

$\log$ is only defined for positive inputs. Therefore taking $2\log x$ is bad when $x$ is negative, but $\log x^2$ is fine as $x^2$ is positive. Therefore the graphs are the same for positive $x$, but different for negative $x$.

Wen
  • 1,966
  • 9
  • 18
1

In general, the "laws" of exponents and logarithms that you know and love are OK for powers and logarithms of positive numbers, but things are more complicated when negative or complex numbers are involved. For example, $(a^b)^c = a^{bc}$: but not when $a = -1$, $b = 2$, $c = 1/2$. To make sense of this, you have to consider multivalued functions in complex analysis.

Robert Israel
  • 448,999
  • I am speechless, I plugged in values and it does not work. Why? Can you point me to readings or an explanation, even to other similar scenarios? I do not recall learning this exception, or maybe I did and I forgot. Now I am skeptical of the grounding that these "laws" have and where they do and do not work. – Sphygmomanometer Dec 12 '17 at 01:39
  • I just looked some more and everywhere that I see power to a power rule for exponents I find no qualification for when a=1,b=2,c=1/2. You'd think that would be important to include, no? – Sphygmomanometer Dec 12 '17 at 01:42