22

  • If $p\implies q$ ("$p$ implies $q$"), then $p$ is a sufficient condition for $q$.

  • If $\lnot p\implies \lnot q$ ("not $p$ implies not $q$"), then $p$ is a necessary condition for $q$.

I don't understand what sufficient and necessary mean in this case. How do you know which one is necessary and which one is sufficient?

Xander Henderson
  • 29,772
cloud9resident
  • 363
  • 4
    Those are the definitions of necessary and of sufficient. – Zhen Lin Dec 11 '12 at 09:37
  • 1
    Are you aware that $\bar p \implies \bar q$ is the logical equivalent of $q \implies p$ ? Do you know what "necessary" and "sufficient" mean in the English language? – DanielV Nov 11 '14 at 08:55

3 Answers3

34

Suppose first that $p$ implies $q$. Then knowing that $p$ is true is sufficient (i.e., enough evidence) for you to conclude that $q$ is true. It’s possible that $q$ could be true even if $p$ weren’t, but having $p$ true ensures that $q$ is also true.

Now suppose that $\text{not-}p$ implies $\text{not-}q$. If you know that $p$ is false, i.e., that $\text{not-}p$ is true, then you know that $\text{not-}q$ is true, i.e., that $q$ is false. Thus, in order for $q$ to be true, $p$ must be true: without that, you automatically get that $q$ is false. In other words, in order for $q$ to be true, it’s necessary that $p$ be true; you can’t have $q$ true while $p$ is false.

Brian M. Scott
  • 616,228
  • 4
    As usual, I will point out that a downvote not accompanied by an explanatory comment is less than useful. – Brian M. Scott Dec 11 '12 at 12:46
  • how do you know that p is true or not? – cloud9resident Dec 12 '12 at 08:44
  • 2
    @cloud9resident: You don’t know. Whether $p$ is true or not is a completely separate issue from whether it is a necessary or sufficient condition for $q$. The latter does not depend in any way on the truth or falsity of $p$. – Brian M. Scott Dec 12 '12 at 08:46
  • But for not p implies not q, in terms of that reasoning, not q doesn't tell you anything about not p because here are different paths to not q? – committedandroider Jan 25 '15 at 22:32
  • @committedandroider: That’s correct. Knowing that $\neg q$ is true tells you nothing about whether $\neg p$ is true or not. – Brian M. Scott Jan 25 '15 at 22:34
  • So knowing q tells you it has to be p? I don't get what you mean by "without that, you automatially get that q is false" – committedandroider Jan 25 '15 at 22:35
  • @committedandroider: Yes, if you know that $\neg p\to\neg q$ and that $q$ is true, then $\neg p$ must be false, and therefore $p$ must be true. \ If $p$ is not true, then $\neg p$ is true, and the implication $\neg p\to\neg q$ (which you are assuming) then automatically guarantees that $\neg q$ is true and hence that $q$ is false. – Brian M. Scott Jan 25 '15 at 22:40
  • And that logic would work with p->q as well because if you know that q is false, then p must be false as well because you're saying p is a sufficient path to q? – committedandroider Jan 25 '15 at 22:45
  • @committedandroider: That’s right. – Brian M. Scott Jan 25 '15 at 22:47
  • @BrianM.Scott One question.Let $f$ be a function defined on a closed and bounded interval $[a,b]$. Then we know a necessary and sufficient condition for Riemann integrable of $f$(say this condition as $Q$) is $f$ is continuous almost everywhere (say this condition as $P$). As you have written that if $P\implies Q$ then $P$ is sufficient condition of $Q$ and $Q$ could be TRUE even $P$ were not true. So there exists an example of a function which is not continuous a.e. but still Riemann integrable. What is that example ? – Empty Sep 09 '17 at 08:02
  • "...but having p true ensures that q is also true." And yet the truth table has an entry for P is true and Q is false. The sheer quantity of writing to convince someone why P⟹Q is true or false is amazing. Something obviously is wrong. Since the math of the logic is correct, it must be the explanations that are at fault. If there was as much verbiage surrounding 1+1=2, we'd still be counting on our fingers! –  Mar 23 '20 at 14:29
  • @Empty: (For some reason I never saw this comment.) When I say that $Q$ could be true even if $P$ is false, I am not saying that such an example must necessarily exist: I am saying that such an example is consistent with $P\to Q$. Obviously if $P$ is a necessary and sufficient condition for $Q$, then $P\leftrightarrow Q$, and no such example can exist. – Brian M. Scott Sep 13 '22 at 21:46
  • @user756686: Any truth table for a proposition involving variables $p$ and $q$ will have a line for $p$ true and $q$ false: that’s simply a fact about the structure of truth tables. It will also have lines for $p$ and $q$ both true, $p$ and $q$ both false, and $p$ false and $q$ true. What is relevant here is that the entry in the column for $p\to q$ in the line $p$ true and $q$ false is F: when $p$ is true and $q$ is false, the implication $p\to q$ is false. There is no problem here whatsoever. – Brian M. Scott Sep 13 '22 at 21:50
24

I always think of it in terms of sets.

enter image description here

In the picture above, for an element to be purple, it's necessary to be red, but it is not sufficient.

The same holds for the blue set, to be in the blue set is a necessary condition in order to be purple, but it is not enough, it's not sufficient.

A sufficient condition is stronger than a necessary condition. If you tell me that you have a red or blue element I can't say for sure if it is in the purple set, but if you tell me that you have a purple element I now for sure that it is in the red and blue sets.

Iocopo
  • 331
1

It has always been difficult for me to connect the linguistic sense of the terms "necessary" and "sufficient" with mathematics. However, with practice with the following table, this skill becomes automatic.

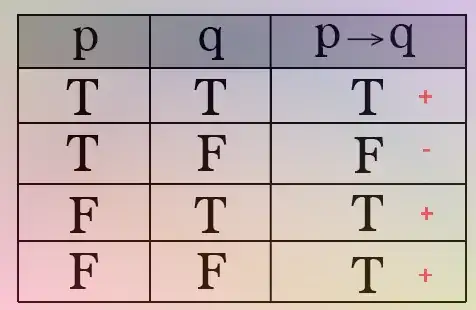
enter image description here

I'm assuming you understand the meaning of the implication. In any case it is helpfull to think about simple example when looking at this table. For example: "If it is raining, then close the window". Then it remains to understand the following.

P is a sufficient for Q. If P is true then Q will be always true (the first line in the table). Note that we do not consider the second line. But as we see in the table Q can be true also when P is false (the third line in the table). So P is "just" a sufficient condition for Q.

Q is a necessary condition for P. It is obvious from the table. P can be true "only" when Q is true (the first line in the table). Note that we do not consider the second line.

About $\lnot A \implies \lnot B$. It is called the contrapositive of the statement $A\implies B$. As you see it is not necessary for you for understanding the "sufficiency" and "necessaty".

Mokhmad-Salekh Khekhaev
  • 745