0

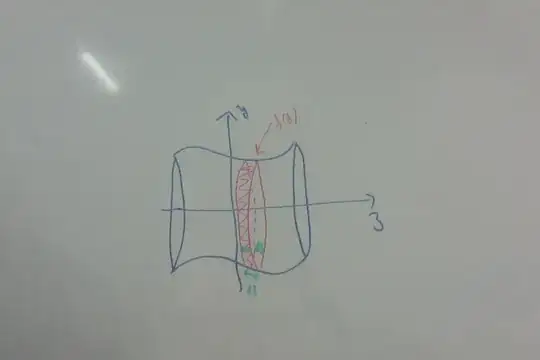
I want to compute the area of a revolution surface generated by $f(x)$, i.e. of the surface $(u, f(u)\cos(v), f(u)\sin(v))$. I know it's $$\mathcal A=\int_{x}^y f(z)\sqrt{1+f'(z)}dz.$$

But why is my argument below wrong :

We sum the area of the infinitesimal cylinder of radius $f(z)$ and altitude $dz$ that should give us $$\int_x^y 2\pi f(z) dz,$$ but this is wrong, so maybe the altitude is in fact $df$, and thus I get $$\int_x^y 2\pi f(z)df=\int_x^y 2\pi f(z)\frac{df}{dz}dz=\int_x^y 2\pi f(z)f'(z)dz,$$ but it still wrong and I don't understand what's wrong in theis logic to sum area of infinitesimal cylinder of radius $f(z)$ and altitude $dz$ or altitude $df$. Could someone explain me ?

enter image description here

user380364
  • 1,947

2 Answers2

1

First, you can realise that both of your formulae cannot be correct: According to the first one, the area of the surface of revolution would only depend on the average value of $f(z)$, but not on the wiggliness (so e.g. $f(z)=1$ and $f(z)=1+\frac{1}{2}\sin\!\left(100*x\right)$ would give the same result). In the second formula, a constant function would give zero area.

But you are on right track: You want to sum "infinitesimal cylinders". However, their area depends on the radius and the length:

  • The radius is $f(z)$.
  • The ("infinitesimal") length depends on the $z$-distance and the variation of $f$ -- you can imagine a riight triangle with sides $\text{d}z$ and $\text{d}f$. Then the hypotenuse has length $$\sqrt{\text{d}z^2+\text{d}f^2}=\sqrt{\text{d}z^2+f'^2\text{d}f^z}=dz\sqrt{1+f'^2}\,,$$ and you've got the integrand -- you are missing a square under the root.

(This argument is somewhat heuristic, but you could turn it into a proper one with limits etc. Not also that your first formula is missing a $2\pi$, and if your limits of integration are $x$ and $y$, you should not label the up-pointing axis in your diagram $y$ as well.)

Toffomat
  • 2,245
1

There is a subtlety: you are not summing cylinders, but cones, so that there needs to be a correction factor. In the 2D section, this correction factor corresponds to the element of arc. So

$$\int f(z)\,ds=\int f(z)\sqrt{1+f'^2(z)}\,dz.$$

You could try to argue "mh, why should I apply this correction when the difference between $dz$ and $ds$ is infinitesimal ?" Well just because the ratio $ds/dz$ is not $1$ and by integration the difference turns to a finite value.

  • and so, if we wanted to have the volume, we would sum cylinder or cone too ? – user380364 Dec 08 '17 at 08:20
  • For the element of volume the situation is different. You are revolving a rectangular area $f(z),dz$ plus a small triangular area $df,dz/2=f'(z)dz^2/2$, which is an infinitesimal of higher order. So the difference between a cylindre and a cone is neglectible. –  Dec 08 '17 at 08:29