6

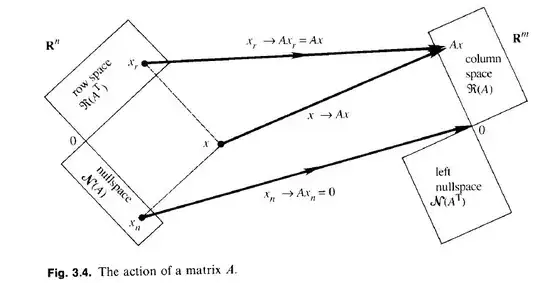
We know that, if $A$ is a linear bounded operator, then $\operatorname{Ker}(A) \perp \operatorname{Range}(A^*)$, where $A^*$ is the adjoint of $A$.

I have no troubles understanding the proof of this (which can be found for example on this answer), however I cannot really understand the intuition behind it.

Is there some way to intuitively understand this result, maybe through geometrical reasoning?

glS
  • 6,818

3 Answers3

5

That's a very interesting question.

From my point of view, the key point lies in the fact that $rank(A)=rank(A^*)$ (i.e. n° of of indipendent columns = n° of indipendent rows) .

As we know, $Ker(A)\subset \mathbb{R^n}$ acts on columns vectors $\in\mathbb{R^m}$ in such way that their combination sum up to the zero vector, thus, as $rank(A)=rank(A^*)$, its orthogonal space must necessarly coincides with ${Range}(A^*)$, then:

$$\operatorname{Ker}(A) \perp \operatorname{Range}(A^*)$$

Here is a famous picture after Prof. G. Strang book on Linear Algebra and the link to his video on the "Big Pictures":

enter image description here

https://www.youtube.com/watch?v=ggWYkes-n6E

I hope it can help your insight on this fact as it is for me.

user
  • 154,566
  • I thought a bit about this and I think I see (at least part of) your point. If $A$ is a matrix, it is actually trivial to see why $\text{Ker}(A)$ is orthogonal to the range of $A^$. Taking inspiration from the linked video: the Ker of $A$ is the set of vectors orthogonal to the complex conjugates of (all) the rows of $A$. But the range of $A^$ is exactly the span of those same rows, hence the spaces are trivially orthogonal to each other. It seems so trivial now that the question itself seems silly, at least for the case of finite dimensional operators (that is, matrices). – glS Dec 11 '17 at 15:49
  • I still don't much see why the fact that the ranks of $A$ and $A^*$ are the same is relevant though – glS Dec 11 '17 at 15:52
2

Thinking of $T: V \to W$ as the linear operator represented by $A$, we have the adjoint map $T^{*}: W^{*} \to V^{*}$ which is represented by $A^{*}$. The adjoint map takes a covector and precomposes it with $T$, and hence every covector so obtained vanishes on the kernel of $T$, giving precisely the vector-covector notion of orthogonality.

Elchanan Solomon
  • 30,807
  • what do you mean here by "precomposes it with $T$"? – glS Dec 05 '17 at 21:17
  • If $\alpha \in W^{}$ is a covector, then $T^{}(\alpha) = \alpha \circ T \in V^{*}$. – Elchanan Solomon Dec 05 '17 at 21:22
  • To clarify, $\alpha$ eats vectors in $W$. To define a covector for $V$, we can take a vector $v \in V$, push it forward to $W$ by $T$ to obtain $T(v)$, and then let $\alpha$ eat that. This composite covector is called $T^{}(\alpha)$ and lives in $V^{}$. – Elchanan Solomon Dec 05 '17 at 21:23
  • all right, I totally see it. You are basically saying that $\text{Range}T^\equiv{\alpha\circ T,:,,\alpha\in W^}$, where $\alpha\circ T\in V^$ is defined as the functional $\alpha\circ T:V\ni v\mapsto \alpha(T(v))$. It follows trivially from this that if $v\in\text{Ker}(T)$ then $v$ will be orthogonal to the rage of $T^$. Thanks for the pointer! – glS Dec 11 '17 at 16:03
1

A very simple way to understand this in finite-dimensional cases might be:

  1. The kernel of $A$ is the space of vectors orthogonal to all its rows.

  2. The range of $A$ is the span of its columns. The range of $A^*$ is the span of the rows of $A$, when $A$ is real. More generally, it's the span of the complex conjugates of the rows of $A$.

  3. Tautologically, the vectors orthogonal to all the rows are orthogonal to the linear combinations of the rows. And this is not affected by the complex conjugate in the point above.

glS
  • 6,818