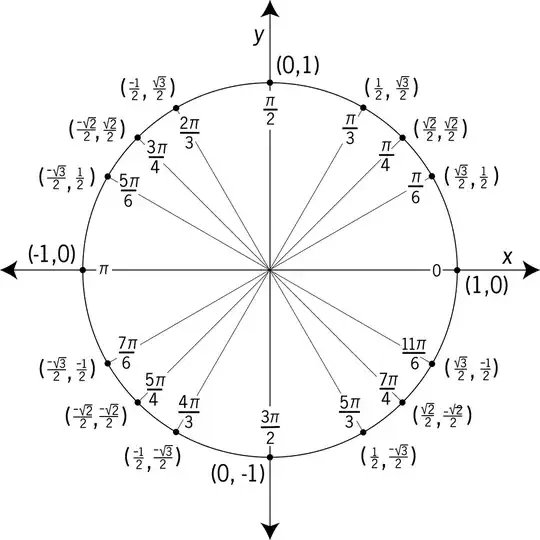
What is a good way to remember the essential angles from the unit circle?
For instance $$\cos\left(\frac{\pi}{4}\right)=\frac{\sqrt{2}}{2} \text{ and } \sin\left(\frac{\pi}{4}\right)=\frac{\sqrt{2}}{2}$$
Asked
Active
Viewed 902 times
0
-
You need only remember $\sin(x)$ for the angles in the region $[0,\frac{\pi}{2}]$ from there it is the rest of the trig relations – Triatticus Dec 05 '17 at 19:46
-
See https://math.stackexchange.com/questions/1553990/easy-way-of-memorizing-values-of-sine-cosine-and-tangent/1554126#1554126 – Jair Taylor Dec 05 '17 at 20:05
-
@Alex5207 If you are ok, you can set as solved. Thanks! – user Dec 06 '17 at 13:30
-
@gimusi - Thanks, it was definitely solved - How can I set as solved? – Alex5207 Dec 06 '17 at 17:50
-
There should be a button somewhere. Thanks! – user Dec 06 '17 at 17:52
-
@Alex5207 Take a look here. Thanks! https://math.meta.stackexchange.com/questions/3286/how-do-i-accept-an-answer – user Dec 16 '17 at 01:08
-
@Alex5207 Please, if you are ok, you can accept the answer and set it as solved. Thanks! – user Jan 22 '18 at 21:33
1 Answers
1
In my opinion the most effective way is to memorize the important ones in the first quadrant and then obtain the others by symmetry.
user
- 154,566
-
In fact you could just memorize the ones in the first octant $(0 \le \theta \le \pi/4)$ and get the rest by symmetry. – Robert Israel Dec 05 '17 at 19:58