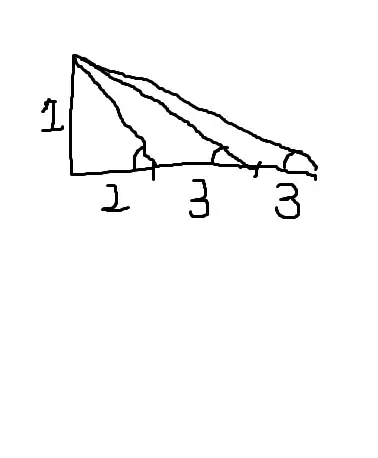
You can also directly use the following formula:
$$\tag{1}\tan(\alpha+\beta+\gamma) = \frac{\tan\alpha+\tan\beta+\tan\gamma-\tan\alpha\tan\beta\tan\gamma}{1-\tan\alpha\tan\beta-\tan\alpha\tan\gamma-\tan\beta\tan\gamma}$$
Taking $\arctan$ of both sides, and setting
$$a:=\tan \alpha, b:=\tan \alpha, c :=\tan \gamma,$$
we obtain:
$$\tag{2}\arctan(a)+\arctan(b)+\arctan(c)=\arctan \left( \frac{a+b+c-abc}{1-ab-ac-bc}\right)$$
It remains to replace $a,b,c$ by their values to obtain
$$\arctan 1=\dfrac{\pi}{4}$$
Remark 1 : A domain of validity of formula (1) is for angles $\alpha, \beta, \gamma \in (0, \pi/2)$ such that $\alpha+\beta+\gamma \in (0, \pi/2)$ as well. Here, these conditions are fulfilled.
Proof of formula (2): (that will explain the presence in (2) of symmetric polynomials $1, \ a+b+c, \ ab+ac+bc,\ abc$).
It is an immediate consequence of the following identity in $\mathbb{C}$:
$$\tag{3}(1+ia)(1+ib)(1+ic)=1+i(a+b+c)+i^2(ab+ac+bc)+i^3 abc$$
Because, taking arguments on both sides of (3), under the condition given in Remark 1 (that avoid adding $+k2\pi$ or $+k\pi$):
$$\arg(1+ia)+\arg(1+ib)+\arg(1+ic)=\arg(1-(ab+ac+bc))+i(a+b+c-abc)$$
which is nothing else than (2).
Remark 2: on the model of (2), one can express a sum of $\arctan$ of any size under a closed form $\arctan(\cdots)$.