Expected time of sequence getting typed when the letters are typed randomly

Question

This question has been asked in an examination of the Indian Statistical Institute, Kolkata for second year Master of Statistics students in the subject Martingale Theory.

Q. Mr.Trump decides to post a random message on the Facebook and starts typing a random sequence $\{U_k\}_{k\geq1}$ of letters such that they are chosen independently and uniformly from the $26$ English alphabets. Find out the expected time of the first appearance of the word "COVFEFE". We may assume that Trump has his caps lock on so that only upper case letters are typed. Assume further that the letters are typed at the rate of one letter per second.

I have no idea as to how to proceed. I will be grateful for any help.

Answer 1

Here is a solution to the COVFEFE problem using a Markov chain. I found this great and easy to understand reference with some background information on Markov Chains from Darthmouth College

The probability to type any letter at any given time is $1/26$. We can create a diagram with the different states the word being typed can be in:

The colours represent the probability to move from one state to another. The COVFEFE state, is an absorbing state. Once it is reached, we're done. We need to calculate the expected time (number of steps) to reach this state.

Using the diagram, you can create the $8 \times 8$ transition matrix $\textbf{P}$, where each element $P_{ij}$ represents the probability to go from state $i$ to $j$:

$$\textbf{P} = \begin{pmatrix} \frac{25}{26} & \frac{1}{26} & & & & & & &\\ \frac{24}{26} & \frac{1}{26} & \frac{1}{26} & & & & & &\\ \frac{24}{26} & \frac{1}{26} & & \frac{1}{26} & & & & &\\ \frac{24}{26} & \frac{1}{26} & & & \frac{1}{26} & & & &\\ \frac{24}{26} & \frac{1}{26} & & & & \frac{1}{26} & & &\\ \frac{24}{26} & \frac{1}{26} & & & & & \frac{1}{26} & &\\ \frac{24}{26} & \frac{1}{26} & & & & & & \frac{1}{26} &\\ & & & & & & & 1 &\\ \end{pmatrix}$$

This matrix is in what is called the canonical form:

$$\textbf{P} = \begin{pmatrix} &\textbf{Q} & \textbf{R} \\ &\textbf{0} & \textbf{I}\\ \end{pmatrix}$$

In this case $\textbf{Q}$ is a $7\times7$ matrix of rows and column 1 to 7 (i.e. states 1 to 7), and $\textbf{I}$ is a $1\times1$ identity matrix. See the reference paragraph 11.2 for a more detailed explanation.

From the transition matrix, you can create the fundamental matrix $\textbf{N}$:

$$\textbf{N} = (\textbf{I} - \textbf{Q})^{-1}$$

($\textbf{I}$ of same dimension as $\textbf{Q}$ here)$. \textbf{N}$ has the property that $\textbf{N} = 1 + \textbf{Q} + \textbf{Q}^2 + ...$ i.e. the entry $ij$ is the expected number of times the system is in state $j$ starting from state $i$.

It's not hard to show that the number of steps needed $t_i$ to get from state $i$ to the bound state is given by a vector $\textbf{t}$

$$\textbf{t} = \textbf{N}\textbf{c}$$

See Theorem 11.4 and 11.5 from the reference for the proof.

The tedious bit is actually calculating $\textbf{N}$. It can be done by hand, but I would suggest using Mathematica or something similar instead. Once you have $\textbf{N}$, you find the number of needed steps is $t_1 = 8031810176$, which is about 4% faster than in the 'wrong' answer!

Answer 2

I'm a little late to the party, but here's my solution:

Let's say we have a word $w$ in an alphabet of size $b$, and we have an infinite stream of random letters. let's say we have a gremlin that runs along the stream up until the first occurrence of the word, and then starts from scratch at the next letter. for example, if $w=aba$ then given the stream $aababaababb$ the gremlin will find $a{\bf aba}baababb$ first, then start over from the next letter and find the next occurence of $w$, $a{\bf aba}ba{\bf aba}bb$. note the gremlin missed a copy of $w$ because it overlapped a copy that it did find.

we can think of the stream as a sequence of "gremlin runs", which are the runs from the point the gremlin starts at to the end of the next occurrence of $w$. for example, in the example the runs are $a{\bf aba}$, $ba{\bf aba}$, with a trailing $bb$ (one can assume there are no trails in the infinite stream case). all the runs are completely independent and have the exact same distribution. if we denote by $L$ the expected length of a gremlin run (which is the quantity we are trying to find), and denote by $\mu$ the density of the occurrences of $w$ that the gremlin finds, we get $L=\frac{1}{\mu}$. (the density is the ratio between how many occurrences the gremlin found to how many letters he read, when taken to infinity.)

whenever our gremlin found the word, it is possible that it missed another instance of $w$ sharing $k$ of the same letters, exactly when the first and last $k$ letters of the word are the same. (for example, for $aba$ the first $a$ is the same as the last $a$ so it's true for $k=1$, so it's possible the gremlin would find ${\bf aba}ba$ and miss the second copy). in that case, there are $|w|-k$ more letters to chose, so the chance of having a missed copy of $w$ sharing $k$ letters is exactly $b^{|w|-k}$.

denote $c_k=1$ if the first and last $k$ letters of $w$ are the same for $1\le k<|w|$ and $c_k=0$ otherwise. also denote $\rho=\sum_{k=1}^{|w|-1}c_k b^{k-|w|}$. so, the density of missed occurrences of $w$ is exactly $\rho\mu$, and the density of occurrences of $w$ is $(1+\rho)\mu$. that's just plainly $b^{-|w|}$, so $\mu=\frac{b^{-|w|}}{1+\rho}$.

therefore, $L=\frac{1}{\mu}=(1+\rho)b^{|w|}=\sum_{k=1}^{|w|-1}c_k b^{k}+b^{|w|}$. if you will, the first and last $|w|$ letters of $w$ are just the word itself, so $c_{|w|}=1$, and $L=\sum_{k=1}^{|w|}c_k b^{k}$.

this would explain why the "covfefe" example gave such a nice answer - $26^7$.

formal sidenote: the strong law of large numbers formally justifies that the densities exist with probability 1 and that everything that was claimed holds with probability 1.

Answer 3

My answer is based on the answer of Mike Spivey on a related question, which uses the probability generating function $G(z)$ of a discrete random variable $X$:

$$G(z) = \sum_{k=0}^{\infty} p(k)z^k $$

where $p$ is the probability mass function of $X$. The probability generating function has the nice property that $E[X] = \lim_{z \to 1-}G'(z)$ (limit from below).

I will adapt Mike's answer for completeness here. Any thoughts would be appreciated, I'm curious to know if my reasoning was correct or if there is a clever way of solving this problem!

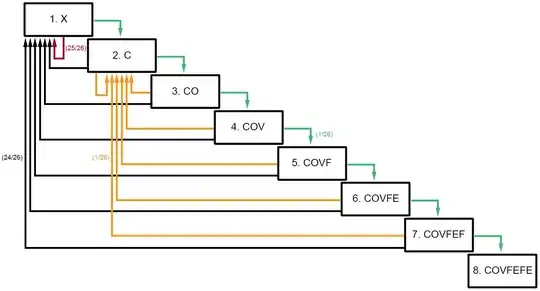
We need a specific sequence of seven characters to form the word "COVFEFE". First a "C", then "O", followed by "V" and so on. We can label the event of typing a correct next character to form the word "COVFEFE" with $S$ and the typing of an incorrect character with $F$. The word "COVFEFE" appearing in a long sequence of characters would then be described by the event $A\cdot SSSSSSS = AS^7$, i.e. a sequence $A$ of any character combination without seven $S$ in a row followed by seven $S$ in a row. Many characters will likely appear before we finally get to $AS^7$. Mr. Trump could type out "COVFEFXCOVFEFE" (the event $S^6FS^7$) or "AAACOVFEFE" ($F^3S^7$), for instance. Undoubtedly, all these character sequences will spark a lively debate on social media if mr. Trump is actually tweeting out nuclear launch codes and impending doom is imminent.

We can look at the situation in the following way. Mr. Trump will play a game of typing random characters, one after another, and the game will end when he types seven $S$ in a row. We need to find the expected number of tries before this happens.

Let $X$ be the probality mass function of the number of characters typed before "COVFEFE" appears. To find the expected number of tries, we need to find the probability generating function of $X$. To find the generating function, look at the infinite sum of possible ways to get seven successes in a row on the last seven tries:

$$S^{7} + FS^{7} + FFS^{7} + SFS^{7} + SSFS^{7} + FSFS^{7} + SFFS^{7} + ...$$

Now, if we were to set $S = pz$ and $F = (1-p)z$, with $p$ the probability of typing the correct next character (and assuming independence), note that we have actually found the probability generating function $G(z)$!

We can rewrite the above expression using a summation and even further simplify using the power sum rule:

$$\sum_{k=0}^{\infty} (F + SF + S^2F + S^3F + S^4F + S^5F + S^6F)^k S^7 = \frac{S^7}{1 - (F + SF + S^2F + S^3 + S^4F + S^5F + S^6F)}$$

If we now substitute $S = pz$ and $F = (1-p)z$, we find:

$$G(z) = \frac{p^7z^7}{1-(1-p)z + (pz)(1-p)z + (pz)^2(1-p)z + (pz)^3(1-p)z + (pz)^3(1-p)z+ (pz)^4(1-p)z + (pz)^5(1-p)z + (pz)^6(1-p)z}$$

At this point we need to find $\lim_{z \to 1-} G'(z)$, which is horrible. I used Wolfram Alpha to do this. The result:

$$E[X] = \frac{1+p+p^2+p^3+p^4+p^5+p^6}{p^7}$$

The probability of typing a correct character is $p = \frac{1}{26}$. Calculating the expected number of characters typed before "COVFEFE" appears, we find $E[X] = 8353082582$. In the case of one character per second, this is the final answer.

Just for fun, I did a little test seeing how many characters I could write out per minute, and it came down to about 300. Mr. Trump says he has pretty big hands, so I'm sure he'll manage 400 CPM. This gives $\frac{8353082582}{400 \cdot 60 \cdot 24 \cdot 365.25}$ which is about 39 years and 8 months, not accounting for sleeping, golf and other responsibilities.