2

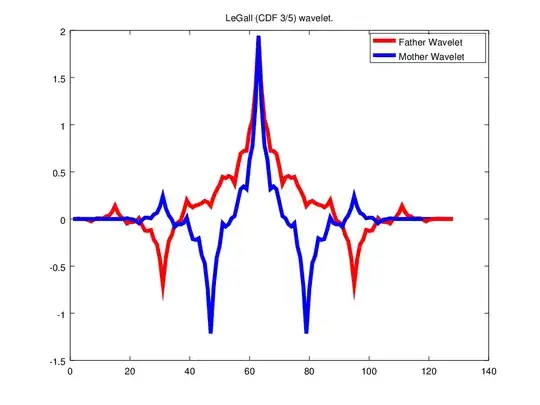
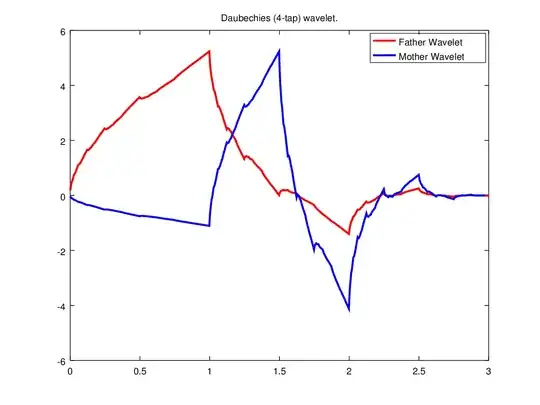
Inspired by this question I got curious if we can find wavelets which have the same property. My suspicion is that for example the functions derived from the Daubechies orthogonal 4 tap filters and the Legall 5/3 functions both express these properties. But how to prove it?

enter image description here

enter image description here

enter image description here

mathreadler
  • 25,824
  • Write everything precisely. – reuns Dec 03 '17 at 01:36
  • It's not really clear to me from reading a Wikipedia article (or any other online source) how to actually compute the value of one of these functions at a point. If this is clarified, then people who understand real analysis but not wavelets can take a stab at your question. – Misha Lavrov Dec 03 '17 at 03:15
  • 2
    $f(x)=\sum_{n\geq 1}\frac{\sin(n^3 x)}{n^2}$ is clearly continuous (it is an absolutely convergent series of continuous functions). To prove its nowhere-differentiability is a bit trickier, but still doable by carefully estimating $f(x)-f(x+\varepsilon)$. If the usual trigonometric functions are replaced by wavelets, there is little to change in the technique. – Jack D'Aurizio Dec 03 '17 at 03:28

1 Answers1

1

From the terrific book of Daubechies, Ten Lectures on Wavelets (see full reference below), Chapter 7, we have that the Daubechies 4-tap refinable function and wavelet are continuous with $\mathrm{H}\ddot{\mathrm{o}}$lder exponent 0.55. However, to quote (in the book, the 4-tap filter is denoted $\!\!\phantom{1}_{2}\phi$):

"In fact, one can even prove that $\!\!\phantom{1}_{2}\phi$ is differentiable in these points, which constitute a set of full measure. This establishes a whole hierarchy of fractal sets... on which $\!\!\phantom{1}_{2}\phi$ has different H$\ddot{\mathrm{o}}$lder exponents." "As a consequence, $\!\!\phantom{1}_{2}\phi$ is left differentiable at dyadic rationals, $x$, but has H$\ddot{\mathrm{o}}$lder exponent .550 when $x$ is approached from the right."

I could not find the exact H$\ddot{\mathrm{o}}$lder exponent or similar analysis for the CDF 5/3, but I did find that its H$\ddot{\mathrm{o}}$lder exponent is at least 0.6584 in the paper "Biorthogonal Bases of Compactly Supported Wavelets" (see full reference below). My hunch would be that the set of points at which the refinable function and wavelet are differentiable has full measure as we saw in the Daubechies 4-tap case, and that at dyadic rationals, rather than the different H$\ddot{\mathrm{o}}$lder coefficients on either side, we would have symmetry (since the refinable function is symmetric, and has a fractal structure).

In Ten Lectures, you can see how one might prove the statements I've given here for the Daubechies orthonormal constructions, and in particular for the 4-tap. You would have to look at "Biorthogonal Bases" for the proof of the result for the CDF 3/5 construction. To be frank, the proofs are quite hard, and the biorthogonal case is harder than the orthonormal case, but you'll learn something from trying to read either or both of them even if you don't come away understanding everything.

  1. I. Daubechies. Ten Lectures on Wavelets. SIAM, Philadelphia, PA, 1992.

  2. A. Cohen, I. Daubechies, and J.-C. Feauveau. "Biorthogonal Bases of Compactly Supported Wavelets." Communications on Pure and Applied Mathematics, 45(5):485-560, June 1992.

RideTheWavelet
  • 3,543