2

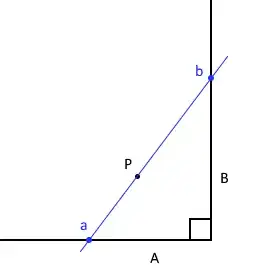
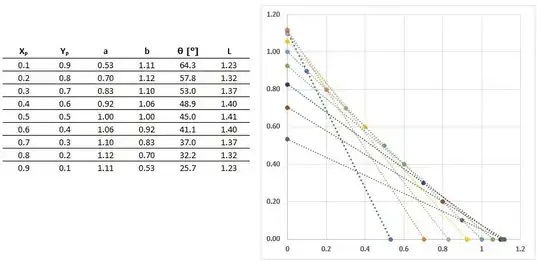
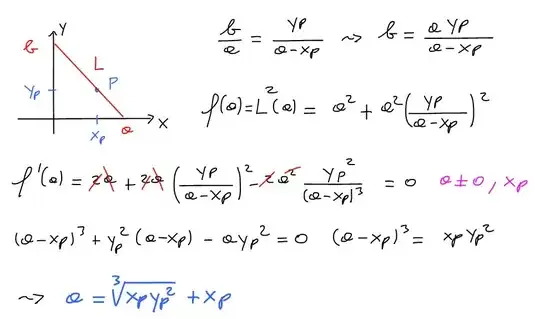Given two perpendicular lines, $A$ and $B$, and a point $p$, I'm trying to find the points $a$ on $A$ and $b$ on $B$, such that $\overline{ab}$ passes through $p$ and is as short as possible.

enter image description here

I'm not very math-y, and my googling has failed to turn up a solution. Is there one?

Sriotchilism O'Zaic
  • 2,228
me--
  • 121
  • Do we know any measurements or coordinates? – randomgirl Dec 01 '17 at 22:31
  • Have you taken calculus? – The Chaz 2.0 Dec 01 '17 at 22:31
  • I think it's worth noting that if the lines $A$ and $B$ are walls of a hallway that goes around a corner, and the point $P$ is the inside corner of that hallway, the shortest possible distance $ab$ is also the length of the longest possible pipe or ladder that can be carried around the corner. And the steps in solving that problem include finding the points $a$ and $b.$ See https://math.stackexchange.com/questions/583707/intuitive-explanation-for-formula-of-maximum-length-of-a-pipe-moving-around-a-co – David K Dec 01 '17 at 23:27
  • @me-- are you ok with the solution? – user Dec 03 '17 at 09:43
  • @me-- you can set as solved if you are ok – user Dec 03 '17 at 10:01
  • Please, if you are ok, you can accept the answer and set it as solved. Thanks! – user Jan 11 '18 at 23:27

2 Answers2

1

Solution can be found by Pythagoras theorem to evaluate the minimum of the lenth square of the segment

here is a derivation of the solution

enter image description here

here is some graph of the solution for $(X_P,Y_P)\in$ line $x+y=1$

enter image description here

user
  • 154,566
  • Thank you I've fixed yhe typo! – user Dec 01 '17 at 23:01
  • The handwriting is not the easiest to read but the result agrees with https://math.stackexchange.com/a/1290503 (specifically, the intermediate step that says $x^3=AB^2$), so I'm reasonably sure it's correct. – David K Dec 01 '17 at 23:33
  • Thanks, I'm preparing some graph to vizualize the solution :) – user Dec 01 '17 at 23:48
0

The equation of any straight line passing through $P(h,k)$ can be set to $$\dfrac{y-k}{x-h}=m$

$$y/(k-mh)-mx/(k-mh)=1$$

We need to minimize $$(k-mh)^2+(k-mh)^2/m^2$$

Now use $$2(a^2+b^2)\le(a+b)^2$$

lab bhattacharjee
  • 274,582