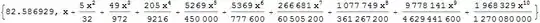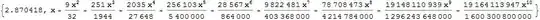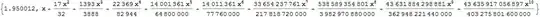This is not an answer to this question but, as I believe, it is a step towards it. Again, let $p\ge 1$ and $q\ge 1$ be integers and $x\in (-1,1)$. Then the following identity holds:
\begin{eqnarray}
&&{\bf H}^{(p)}_q(x)=\\
&&Li_p(x) Li_q(x) + Li_{p+q}(x) + \\
&&\sum\limits_{j=1}^{p-1} (-1)^j \binom{q+j-1}{j} Li_{q+j}(x) Li_{p-j}(x)+\\
&&(-1)^p\sum\limits_{j=p}^{q+p-1} \binom{j-1}{p-1} Li_{q-j+p}(x) Li_j(x)+\\
&&\sum\limits_{j_2=0}^{q-1} [\log(x)]^{j_2} \cdot \sum\limits_{j=p}^{(q+p-1-j_2)} \sum\limits_{j_1=1}^{(q+p-j-j_2)} \frac{(-1)^{q+1-j-j_1-j_2}}{(j_2)!(q+p-j-j_1-j_2)!} \binom{j-1}{p-1} \cdot \\
&&\int\limits_0^x [\log(t)]^{q+p-j-j_1-j_2} \cdot \frac{Li_{j_1}(t) Li_{j-1}(t)}{t} dt
\end{eqnarray}
I have derived this identity using integration by parts. Below is a piece of Mathematica's code that verifies it:
M = 1000;
x = RandomReal[{-1, 1}, WorkingPrecision -> 50];
AA = Map[N[Take[Accumulate[#], -5], 30] &,
Table[HarmonicNumber[n, p] x^n/n^q, {p, 1, 5}, {q, 1, 5}, {n, 1,
M}], {2}];
AA1 = Table[
PolyLog[q, x] PolyLog[p, x] + PolyLog[q + p, x] +
Sum[(-1)^j Binomial[q + j - 1, j] PolyLog[p - j, x] PolyLog[q + j,
x], {j, 1, p - 1}] + (-1)^p Sum[
Binomial[j - 1, p - 1] PolyLog[q - j + p, x] PolyLog[j, x], {j,
p, q + p - 1}] +
Sum[ Log[x]^j2 ((-1)^(
q + 1 - j - j2 + j1)) /((j2)! (q + p - j - j2 - j1)!)
Binomial[j - 1, p - 1] NIntegrate[
Log[t]^(q + p - j - j1 - j2) (
PolyLog[j1, t] PolyLog[j - 1, t])/t , {t, 0, x},
WorkingPrecision :> 30], {j2, 0, q - 1}, {j, p,
q + p - 1 - j2}, {j1, 1, q + p - j - j2}], {p, 1, 5}, {q, 1,
5}];
MatrixForm[#] & /@ {AA1, AA[[All, All, -1]] - AA1}
After running it we are getting a following output:

Now let us take $p=1$ and $q=4$. Then we have:
\begin{equation}
{\bf H}^{(1)}_4(x)= -2 Li_2(x) Li_3(x)+ \log(1-x) Li_4(x) + Li_5(x) + \sum\limits_{j_2=0}^3 [\log(x)]^{j_2} {\mathcal s}_{4-j_2}
\end{equation}
where
\begin{eqnarray}
{\mathcal s}_1&=&\frac{1}{12} \log(1-x)^2\\
{\mathcal s}_2&=&\frac{1}{12} \left(-6 \text{Li}_3(1-x)-12 \text{Li}_2(x) \log (1-x)-6 \log (x) \log ^2(1-x)+\pi ^2 \log (1-x)+6 \zeta (3)\right)\\
{\mathcal s}_3&=&\text{Li}_2(x){}^2-\text{Li}_4(1-x)+\text{Li}_4(x)+\text{Li}_4\left(\frac{x}{x-1}\right)+2 \text{Li}_2(x) \log (x) \log (1-x)-2 \text{Li}_3(x) \log (1-x)+\text{Li}_3(1-x) \log (x)+\zeta (3) \log (1-x)-\zeta (3) \log
(x)+\frac{1}{24} \log ^4(1-x)-\frac{1}{6} \log (x) \log ^3(1-x)+\frac{3}{4} \log ^2(x) \log ^2(1-x)+\frac{1}{12} \pi ^2 \log ^2(1-x)-\frac{1}{6} \pi ^2 \log (x) \log (1-x)+\frac{\pi ^4}{90}\\
{\mathcal s}_4&=&-\frac{1}{12} \log (1-x) \left(12 \text{Li}_4(x)-12 \text{Li}_3(x) \log (x)+\log (1-x) \log ^3(x)\right)+\text{Li}_2(x) \left(2 \text{Li}_3(x)-\frac{3}{4} \log (1-x) \log ^2(x)\right)-\frac{5}{4} \text{Li}_2(x){}^2 \log (x)+\frac{1}{4}\left( {\mathcal S}^{(2)}_2(x) - {\mathcal D}^{(2)}_2(x)\right)
\end{eqnarray}
Below is the Mathematica code that verifies the expression above:
x =.; t =.;
S22[x_] := Integrate[ PolyLog[2, t]^2/t, {t, 0, x}];
D22[x_] := Integrate[(Log[t]^2 PolyLog[2, t])/ (1 - t), {t, 0, x}];
ss := {1/12 Log[1 - x]^2,
1/12 (\[Pi]^2 Log[1 - x] - 6 Log[1 - x]^2 Log[x] -
12 Log[1 - x] PolyLog[2, x] - 6 PolyLog[3, 1 - x] +
6 Zeta[3]), \[Pi]^4/90 + 1/12 \[Pi]^2 Log[1 - x]^2 +
1/24 Log[1 - x]^4 - 1/6 \[Pi]^2 Log[1 - x] Log[x] -
1/6 Log[1 - x]^3 Log[x] + 3/4 Log[1 - x]^2 Log[x]^2 +
2 Log[1 - x] Log[x] PolyLog[2, x] + PolyLog[2, x]^2 +
Log[x] PolyLog[3, 1 - x] - 2 Log[1 - x] PolyLog[3, x] -
PolyLog[4, 1 - x] + PolyLog[4, x] + PolyLog[4, x/(-1 + x)] +
Log[1 - x] Zeta[3] - Log[x] Zeta[3],
-(5/4) Log[x] PolyLog[2, x]^2 +
PolyLog[2, x] (-(3/4) Log[1 - x] Log[x]^2 + 2 PolyLog[3, x]) -
1/12 Log[
1 - x] (Log[1 - x] Log[x]^3 - 12 Log[x] PolyLog[3, x] +
12 PolyLog[4, x]) + 1/4 (-D22[x] + S22[x])};
{p, q} = {1, 4};
{t0, dummy} = Timing[Simplify[Normal[Series[
-2 PolyLog[2, x] PolyLog[3, x] + Log[1 - x] PolyLog[4, x] +
PolyLog[5, x] +
Total[Table[Log[x]^j2 ss[[4 - j2]], {j2, 0, q - 1}]], {x, 0,
3}]], Assumptions -> -1 < x < 1]]
If you run that code after about 105 seconds Mathematica 9.0 produces the following result:

as it should be.
Likewise let us take $p=2$ and $q=3$ then we have:
\begin{equation}
{\bf H}^{(2)}_3(x) = 4 Li_2(x) Li_3(x) +Li_5(x) + \sum\limits_{j_2=0}^2 [\log(x)]^{j_2} {\mathcal s}_{3-j_2}
\end{equation}
where
\begin{eqnarray}
{\mathcal s}_1 &=& \text{Li}_3(1-x)-\text{Li}_2(1-x) \log (1-x)-\frac{1}{2} \log (x) \log ^2(1-x)-\zeta (3)\\
{\mathcal s}_2 &=& -\frac{3 \text{Li}_2(x){}^2}{2}+2 \text{Li}_4(1-x)-2 \text{Li}_4(x)-2 \text{Li}_4\left(\frac{x}{x-1}\right)-2 \text{Li}_2(x) \log (x) \log (1-x)+2 \text{Li}_3(x) \log (1-x)-2 \text{Li}_3(1-x) \log (x)-2 \zeta (3) \log
(1-x)+2 \zeta (3) \log (x)-\frac{1}{12} \log ^4(1-x)+\frac{1}{3} \log (x) \log ^3(1-x)-\log ^2(x) \log ^2(1-x)-\frac{1}{6} \pi ^2 \log ^2(1-x)+\frac{1}{3} \pi ^2 \log (x) \log (1-x)-\frac{\pi ^4}{45}\\
{\mathcal s}_3 &=& \frac{1}{2} \text{Li}_2(x) \left(-8 \text{Li}_3(x)+4 \text{Li}_2(x) \log (x)+\log (1-x) \log ^2(x)\right)+ \frac{1}{2} {\mathcal D}^{(2)}_2(x)
\end{eqnarray}
Again , below is the Mathematica code that verifies that:
{p, q} = {2, 3}; x =.; t =.;
D22[x_] := Integrate[(Log[t]^2 PolyLog[2, t])/ (1 - t), {t, 0, x}];
ss := {-(1/2) Log[1 - x]^2 Log[x] - Log[1 - x] PolyLog[2, 1 - x] +
PolyLog[3, 1 - x] - Zeta[3], -(\[Pi]^4/45) -
1/6 \[Pi]^2 Log[1 - x]^2 - 1/12 Log[1 - x]^4 +
1/3 \[Pi]^2 Log[1 - x] Log[x] + 1/3 Log[1 - x]^3 Log[x] -
Log[1 - x]^2 Log[x]^2 - 2 Log[1 - x] Log[x] PolyLog[2, x] -
3/2 PolyLog[2, x]^2 - 2 Log[x] PolyLog[3, 1 - x] +
2 Log[1 - x] PolyLog[3, x] + 2 PolyLog[4, 1 - x] -
2 PolyLog[4, x] - 2 PolyLog[4, x/(-1 + x)] -
2 Log[1 - x] Zeta[3] + 2 Log[x] Zeta[3],
1/2 PolyLog[2,
x] (Log[1 - x] Log[x]^2 + 4 Log[x] PolyLog[2, x] -
8 PolyLog[3, x]) + 1/2 D22[x]};
{t0, dummy} =
Timing[Simplify[
Normal[Series[
4 PolyLog[2, x] PolyLog[3, x] + PolyLog[5, x] +
Total[Table[Log[x]^j2 ss[[3 - j2]], {j2, 0, q - 1}]], {x, 0,
10}]], Assumptions -> 0 < x < 1]]
The output being:
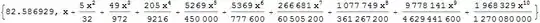
Now let us take $p=3$ and $q=2$. Then we have:
\begin{equation}
{\bf H}^{(3)}_2(x) = -2 Li_2(x) Li_3(x)+Li_5(x) + \sum\limits_{j_2=0}^1 [\log(x)]^{j_2} {\mathcal s}_{2-j_2}
\end{equation}
where
\begin{eqnarray}
{\mathcal s}_1 &=& \frac{1}{2} [Li_2(x)]^2 \\
{\mathcal s}_2 &=& -\frac{1}{2} \log(x) Li_2(x)^2 + 3 Li_2(x) Li_3(x) - \frac{3}{2} {\mathcal S}^{(2)}_2(x)
\end{eqnarray}
The code that verifies this along with its output are below:
{p, q} = {3, 2}; x =.; t =.;
S22[x_] := Integrate[ PolyLog[2, t]^2/t, {t, 0, x}];
ss := {1/2 PolyLog[2, x]^2, -1/2 Log[x] PolyLog[2, x]^2 +
3 PolyLog[2, x] PolyLog[3, x] - 3/2 S22[x]};
{t0, dummy} =
Timing[Simplify[
Normal[Series[-2 PolyLog[2, x] PolyLog[3, x] + PolyLog[5, x] +
Total[Table[Log[x]^j2 ss[[2 - j2]], {j2, 0, q - 1}]], {x, 0,
10}]], Assumptions -> 0 < x < 1]]
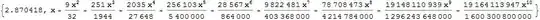
Finally let us take $p=4$ and $q=1$. Then we have:
\begin{equation}
{\bf H}^{(4)}_1(x) = -\log(1-x) Li_4(x) + Li_5(x) + \sum\limits_{j_2=0}^0 [\log(x)]^{j_2} {\mathcal s}_{1-j_2}
\end{equation}
where
\begin{eqnarray}
{\mathcal s}_1 &=& -Li_2(x) Li_3(x) + {\mathcal S}^{(2)}_2(x)
\end{eqnarray}
with the code and its output given below:
{p, q} = {4, 1}; x =.; t =.;
S22[x_] := Integrate[ PolyLog[2, t]^2/t, {t, 0, x}];
ss := {-PolyLog[2, x] PolyLog[3, x] + S22[x]}
{t0, dummy} =
Timing[Simplify[
Normal[Series[-Log[1 - x] PolyLog[4, x] + PolyLog[5, x] +
Total[Table[Log[x]^j2 ss[[1 - j2]], {j2, 0, q - 1}]], {x, 0,
10}]], Assumptions -> 0 < x < 1]]
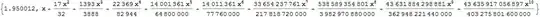
The overall conclusion from this exercise is that whenever $p+q\ge 5$ the generating functions in question cannot be reduced to poly-logarithms only. If $p+q=5$ then the additional quantities that enter are ${\mathcal S}^{(2)}_2(x)$ and ${\mathcal D}^{(2)}_2(x)$ which themselves are independent from each other and also cannot be reduced to other generating functions.