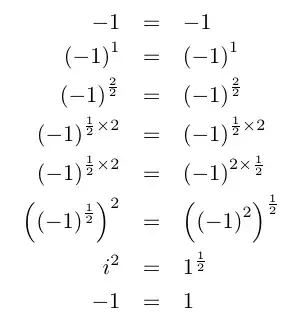$ \sqrt{(-1)^2} \overset{?}{\ne} (\sqrt{-1})^2.\; $ Which of the following steps is wrong:

Question

Which of the following steps is wrong?

Answer 1

For x a positive real numbers, $\sqrt[b]{x^a}= x^{a/b}= (x^{1/b})^a$. But that is not true for x a negative number when the root might be imaginary.

Answer 2

When you work with complex numbers,the square root isn't an operation that gives you just one value, it gives you 2 different values (a number and its opposite). So the square root of 1 can either be 1 or -1.

Answer 3

The issue you are having is that taking roots is not a well defined function. Note that both $-1$ and $1$ are suitable answers to $ \sqrt{(-1)^2} $.

In particular, in the second to last step you are choosing a specific root for each argument, choosing $1$ instead of $-1$ for $((-1)^2)^\frac{1}{2}$.

For a better understanding of this idea, look up roots of unity.

Answer 4

I think we can not say $(i^2)^{1/2}=(i^{1/2})^2 $in this case :

As : $\sqrt{x^2}\neq (\sqrt{x})^2$ In complex numbers

Answer 5

in the complex $\sqrt{1}=\pm1$ thus equality holds, even if a solution has been lost

to better explain why a solution has been lost lets consider a generic complex number $w$

case 1: $\sqrt{w}=z_1,z_2 \rightarrow z^2_1,z^2_2=w$

case 2: $w^2=v \rightarrow \sqrt{v}=w_1,w_2$

and at least one between $w_1,w_2$ is equal to $w$.