Does there exist a closed form for the sinc function series $\sum_{n=1}^\infty \frac{\sin\sqrt{n^2+1}}{\sqrt{n^2+1}}$?

Question

Here I want to get the closed form solution of the following summation

$$ \sum_{n=1}^\infty \frac{\sin\sqrt{n^2+1}}{\sqrt{n^2+1}} \qquad(1) $$

Or the more general form ($x$ be an arbitrary real number, and $a\geq0$ is a constant):

$$ f_a(x) = \sum_{n=1}^\infty \frac{\sin\left(x\sqrt{n^2+a^2}\right)}{\sqrt{n^2+a^2}}\qquad(2) $$

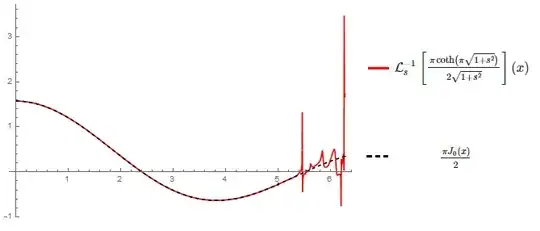
I tried the numeircal simulations before I post the question. I truncated the first $1,000,000$ terms of equation (1) and it turned $0.781233190560320$.

Anyone can help me?

In fact, I made it the reduced case when $a=0$. It can be proved by Fourier series: $$ f_0(x)=\sum_{n=1}^\infty \frac{\sin nx}{n} = \left\{ \matrix{\dfrac{\pi-x}{2}, 0<x<2\pi\\0, x=0,2\pi} \right. $$ And the function is periodical: $$ f_0(x) = f_0(x+2\pi) $$

Edit: How about this one? $$ g_a(x) = \sum_{n=1}^\infty \frac{\cos\left(x\sqrt{n^2+a^2}\right)}{\sqrt{n^2+a^2}}\qquad(3) $$

We get the "diverging wave solution" in physics when we combine the equation (2) and (3): $$ h_a(x)=g_a(x)+\text{i}f_a(x)=\sum_{n=1}^\infty \frac{\exp\left(\text{i}x\sqrt{n^2+a^2}\right)}{\sqrt{n^2+a^2}}\qquad(4) $$

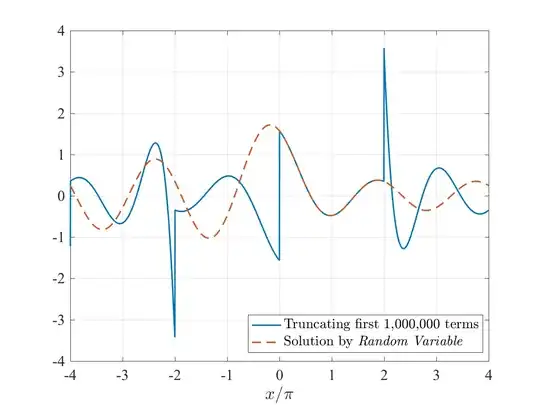
Edit #2: I tested the solution solved by Random Variable (see the most ranked answer and thousands thanks to it!) compared with the truncating results:

$$ \sum_{n=1}^N\frac{\sin \left(x\sqrt{n^2+a^2}\right)}{\sqrt{n^2+a^2}}, N = 1,000,000, a=1 $$

Here is the solution by @Random Variable: the solution of equation (2) as the following:

$$ \sum_{n={1}}^\infty \frac{\sin\left(x\sqrt{n^2+a^2}\right)}{\sqrt{n^2+a^2}} = \frac{\pi}{2} J_0(ax) -\frac{\sin(ax)}{2a}, a>0, 0<x<2\pi\qquad(2*) $$ where $J_0(ax)$ is the Bessel function of the first kind of order zero.

Here is the comparison:

It can be found that the both agree well when $0 <x<2\pi$,but differ in other domain. So, how about the solution beyond $(0,2\pi)$?

Edit #3:

Inspired by Random Variable's answer, I found the solution of equation (3) as the following:

$$ \sum_{n={1}}^\infty \frac{\cos\left(x\sqrt{n^2+a^2}\right)}{\sqrt{n^2+a^2}} = -\frac{\pi}{2} Y_0(ax) -\frac{\cos(ax)}{2a}, a>0, 0<x<2\pi\qquad(3*) $$ where $Y_0(ax)$ is the Bessel function of the second kind of order zero.

Here is the comparison: 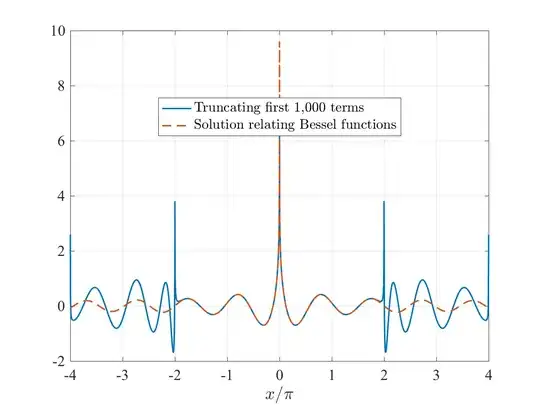Note that equation (3) is divergent when $x=0$.

---

Possible relating QUESTIONS:

Does there exist a closed form for the non-integer shifted sinc-function series: $\frac{\sin(n+a)x}{(n+a)x}$?

Answer 1

UPDATE:

To apply the Abel-Plana formula, the behavior of $f(z)$ as $\Re (z) \to + \infty$ is also important. This was omitted from my answer.

A sufficient condition, now stated here, is $f(z) \sim O(e^{2\pi|\Im z|}/|z|^{1+\epsilon}) $ as $\Re(z) \to +\infty$.

The function $\frac{\sin \left( x\sqrt{z^{2}+a^{2}}\right)}{\sqrt{z^{2}+a^{2}}} $ does not satisfy this condition.

But as achille hui explains in the linked answer, this condition is about ensuring that $\lim_{b\to\infty} f(b) = 0$ and $$\lim_{b\to\infty}\int_0^\infty \frac{f(b+it)-f(b-it)}{e^{2\pi t} - 1}dt = 0. $$

I've asked achille hui to post an answer to show that the limit of the above integral is indeed going to zero.

---

We can use the the Abel-Plana formula as stated in achille hui's answer here.

First notice that the singularities of $f(z) = \frac{\sin \left( x\sqrt{z^{2}+a^{2}}\right)}{\sqrt{z^{2}+a^{2}}}$ are removable.

Also, for $x>0$, $\left|\sin \left( x\sqrt{z^{2}+a^{2}}\right)\right| \sim \frac{e^{x\left|\Im (z)\right|}}{2} $as $\Im(z) \to \pm \infty$.

So if $0 < x < 2 \pi$, the conditions of the Abel-Plana formula are satisfied, and we get $$\begin{align} \sum_{{\color{red}{n=0}}}^{\infty} \frac{\sin \left( x\sqrt{n^{2}+a^{2}}\right)}{\sqrt{n^{2}+a^{2}}} &= \int_{0}^{\infty} \frac{\sin \left( x\sqrt{t^{2}+a^{2}}\right)}{\sqrt{t^{2}+a^{2}}} \, dt + \frac{1}{2} f(0) + i (0) \\ &= \int_{0}^{\infty} \frac{\sin \left( x\sqrt{t^{2}+a^{2}}\right)}{\sqrt{t^{2}+a^{2}}} \, dt + \frac{\sin (ax)}{2a}. \end{align}$$

But from this answer, we know that $$\int_{0}^{\infty} \frac{\sin \left( x\sqrt{t^{2}+a^{2}}\right)}{\sqrt{t^{2}+a^{2}}} \, dt = \frac{\pi}{2} J_{0}(ax), \quad (a>0, \ x>0), \tag{1}$$ where $J_{0}(x)$ is the Bessel function of the first kind of order zero.

(To see that $(1)$ is related to the Mehler–Sonine integral representation of the Bessel function of the first kind, you only need to make the initial substitution in that answer).

Therefore, $$\sum_{{\color{red}{n=0}}}^{\infty} \frac{\sin \left( x\sqrt{n^{2}+a^{2}}\right)}{\sqrt{n^{2}+a^{2}}} = \frac{\pi}{2} J_{0}(ax) + \frac{\sin (ax)}{2a}, \quad (a>0, \ 0<x < 2 \pi).$$

To recover the $a=0$ case, pull out the $n=0$ term and take the limit on both sides of the equation as $a \to 0^{+}$.

---

It should be noted that the series converges by Dirichlet's test since $$\sin \left( x\sqrt{t^{2}+a^{2}}\right) \sim \sin(tx) + \mathcal{O} \left(\frac{1}{t} \right)$$ as $t \to \infty$, which can be shown by expanding $\sqrt{t^{2}+a^{2}} = t \sqrt{1+ \frac{a^{2}}{t^{2}}}$ at $t= \infty$ and using the trig identity for $\sin(\alpha +\beta)$.

Answer 2

Per request, this is a supplement to Random Variable's answer.

In Frank W. J Olver's book: Asymptotics and Special Functions, the Abel-Plana formula on finite sum appears in essentially following form:

Let $S$ be the strip $a \le \Re z \le b$ where $a, b \in \mathbb{N}$. For any function $f(z)$

1. continuous on $S$ and analytic on interior of $S$.
2. $f(z) \sim o(e^{2\pi|\Im z|} )$ as $\Im z \to \pm \infty$, uniformly with respect to $\Re z$.

We have $$\begin{align}\sum_{n=a}^b f(n) = &\int_a^b f(x) dx + \frac12\left( f(a) + f(b)\right) \\& + i \int_0^\infty \frac{f(a+it) - f(a-it) - f(b+it) + f(b-it)}{e^{2\pi t}-1} dt\end{align}$$

For $f(z) = \frac{\sin(x\sqrt{z^2+a^2})}{\sqrt{z^2+a^2}}$ with $0 < x < 2\pi$, above conditions is satisfied for $a = 0$ and any $b \in \mathbb{Z}$. To obtain the version of AP formula for infinite sum used in Random Variable's answer, we just need:

$$\lim_{b\to \infty}f(b) = 0\quad\text{ and }\quad \lim_{b\to\infty}\int_0^\infty \frac{f(b+it) - f(b-it)}{e^{2\pi t}-1} dt = 0$$ The first condition is trivial. For the second condition, notice for any $n > 0$, $$\left|\sqrt{(n\pm it)^2+a^2}\right| = \left|\sqrt{(n \pm i(t+a))(n \pm i(t-a))}\right| \ge n$$ We find for large $b$ and $t$, $$\frac{\left|f(b\pm it)\right|}{e^{2\pi t}-1} \le \frac{\left|\sin\left(x(b\pm it) + O\left(\frac{a^2}{b}\right)\right)\right|}{b(e^{2\pi t}-1)} \sim \frac{1}{2b}e^{-(2\pi - x)t}\left( 1 + O\left(\frac{a^2}{b}\right)\right) $$ For large $b$ but small $t$, we have $$\frac{\left|f(b + it) - f(b - it)\right|}{e^{2\pi t}-1} \sim O\left(\frac{1}{b}\right)$$ instead (the pole at $t = 0$ from denominator is cancelled by the differences in numerator).

Combine these, we have following estimate of the integral appears in second condition:

$$\int_0^\infty \frac{f(b+it)-f(b-it)}{e^{2\pi t}-1} dt = O\left(\frac{1}{b(2\pi - x)}\right)$$ The second condition is satisfied and the use of AP formula in answering this question is justified.

Answer 3

To go beyond the limitation $-2\pi<x<2\pi$ for the sine series, we can use the representation G&R (6.677.6) (or Ederlyi TI p.57 1.13.47) \begin{equation} \frac{\sin x\sqrt{n^2+a^2}}{\sqrt{n^2+a^2}}=\int_0^x J_0\left( n\sqrt{x^2-t^2} \right)\cos at\,dt\tag{1} \end{equation} valid for $x>0$. (For $x<0$, we will use the fact that the series is an odd function of $x$, as remarked by @RandomVariable). The summation can be computed using the Schlömilch series (G&R 8.521.1): \begin{equation} \sum_{n=1}^\infty J_0(nz)=-\frac{1}{2}+\frac{1}{z}+2\sum_{m=1}^p\frac{1}{\sqrt{z^2-4\pi^2m^2\pi^2}} \end{equation} for $2p\pi<z<2(p+1)\pi$, which defines $p=\lfloor \frac{z}{2\pi}\rfloor$. Choosing $z=\sqrt{x^2-t^2}$, \begin{align} S(x)&=\sum_{n=1}^\infty\frac{\sin x\sqrt{n^2+a^2}}{\sqrt{n^2+a^2}}\\ &=\int_0^x\sum_{n=1}^\infty J_0\left( n\sqrt{x^2-t^2} \right)\cos at\,dt\\ &=\int_0^x\left[-\frac{1}{2}+\frac{1}{\sqrt{x^2-t^2}}+2\sum_{m=1}^{\lfloor \frac{\sqrt{x^2-t^2}}{2\pi}\rfloor}\frac{1}{\sqrt{x^2-t^2-4\pi^2m^2\pi^2}}\right] \cos at\,dt\\ &=\int_0^x\left[-\frac{1}{2}+\frac{1}{\sqrt{x^2-t^2}}\right]\cos at\,dt+2\sum_{1\le m< \lfloor \frac{x}{2\pi}\rfloor}\int_0^{\sqrt{x^2-4\pi^2m^2}}\frac{\cos at\,dt}{\sqrt{x^2-4\pi^2m^2-t^2}} \end{align} (The summation does not exist if $\lfloor \frac{x}{2\pi}\rfloor=0$). With the classic integral representation \begin{equation} \frac{\pi}{2}J_0(s)=\int_0^1\frac{\cos sx}{\sqrt{1-x^2}}\,dx \end{equation} the result can be written as \begin{equation} \sum_{n=1}^\infty\frac{\sin x\sqrt{n^2+a^2}}{\sqrt{n^2+a^2}}=\frac{\pi}{2}J_0(ax)-\frac{\sin ax}{2a}+\pi\sum_{1\le m< \lfloor \frac{x}{2\pi}\rfloor}J_0\left( a\sqrt{x^2-4\pi^2m^2-t^2}\right) \end{equation} which seems to be numerically correct. Unfortunately, no corresponding form of (1) for the cosines seems to exist.

Answer 4

COMMENT to users: Achille-Hui and Random-Variable

How about this ?:

$$\sum _{n=0}^{\infty } \frac{\sin \left(x \sqrt{n^2+a^2}\right)}{\sqrt{n^2+a^2}}=\frac{1}{2} \pi J_0(a x)+\frac{\sin (a x)}{2 a}$$

$$\sum _{n=0}^{\infty } \mathcal{L}_x\left[\frac{\sin \left(x \sqrt{n^2+a^2}\right)}{\sqrt{n^2+a^2}}\right](s)=\frac{1}{2} \pi J_0(a x)+\frac{\sin (a x)}{2 a}$$

$$\mathcal{L}_s^{-1}\left[\sum _{n=0}^{\infty } \frac{1}{a^2+n^2+s^2}\right](x)=\frac{1}{2} \pi J_0(a x)+\frac{\sin (a x)}{2 a}$$

$$\mathcal{L}_s^{-1}\left[\frac{1}{2 \left(a^2+s^2\right)}+\frac{\pi \sqrt{-a^2-s^2} \cot \left(\pi \sqrt{-a^2-s^2}\right)}{2 \left(a^2+s^2\right)}\right](x)=\frac{1}{2} \pi J_0(a x)+\frac{\sin (a x)}{2 a}$$

$$\mathcal{L}_s^{-1}\left[\frac{1}{2 \left(a^2+s^2\right)}\right](x)+\mathcal{L}_s^{-1}\left[-\frac{\pi \cot \left(\pi \sqrt{-a^2-s^2}\right)}{2 \sqrt{-a^2-s^2}}\right](x)=\frac{1}{2} \pi J_0(a x)+\frac{\sin (a x)}{2 a}$$

for $a>0$ and $s>0$

$$\frac{\sin (a x)}{2 a}+\mathcal{L}_s^{-1}\left[\frac{\pi \coth \left(\pi \sqrt{a^2+s^2}\right)}{2 \sqrt{a^2+s^2}}\right](x)=\frac{1}{2} \pi J_0(a x)+\frac{\sin (a x)}{2 a}$$ $$\mathcal{L}_s^{-1}\left[\frac{\pi \coth \left(\pi \sqrt{a^2+s^2}\right)}{2 \sqrt{a^2+s^2}}\right](x)=\frac{1}{2} \pi J_0(a x)$$

$$\mathcal{L}_x\left[\mathcal{L}_s^{-1}\left[\frac{\pi \coth \left(\pi \sqrt{a^2+s^2}\right)}{2 \sqrt{a^2+s^2}}\right](x)\right](s)=\mathcal{L}_x\left[\frac{1}{2} \pi J_0(a x)\right](s)$$

$$\frac{\pi \coth \left(\pi \sqrt{a^2+s^2}\right)}{2 \sqrt{a^2+s^2}}\neq \frac{\pi }{2 \sqrt{a^2+s^2}}$$

and then:

$$\sum _{n=0}^{\infty } \frac{\sin \left(x \sqrt{n^2+a^2}\right)}{\sqrt{n^2+a^2}}\neq \frac{1}{2} \pi J_0(a x)+\frac{\sin (a x)}{2 a}$$

EDITED:

Comparison a numeric InverseLaplaceTransform and Bessel function: