Consider the sequence $f_n(x)$ defined by $f_0(x) = \sin x$, $f_1(x) = \sin\cos x$, $f_2(x) = \sin\cos\sin x$, and so on. One can check that $f_n(x)$ converges to a constant, say $N_p$.
My question is what might be the value of $N_p$? By brute force I got $N_p=0.69481969\ldots.$
Why does $\sin\left(\cos(\ldots\sin(\cos(x)))\right)$ converge to a constant?
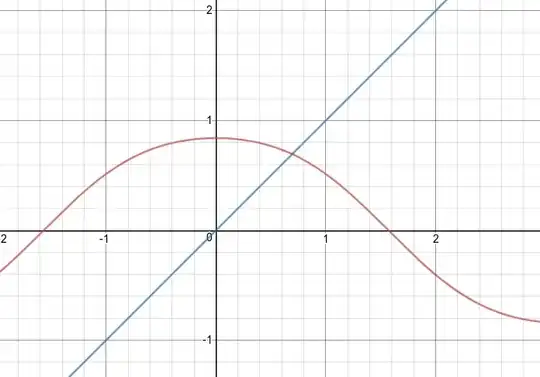
It's easier to represent this sequence as follows: $x_0=0,x_{n+1}=\sin(\cos(x_n))$. The value this sequence converges to is called a fixed point. A fixed point, $x$, of the function $f$, is a value such that $f(x)=x$. In your case, $f(x)=\sin(\cos(x))$. The fixed point could be interpreted, with the figure below, where the red curve is $y=f(x)$ and the blue line is $y=x$. The point of intersection of the line and the curve is the fixed point. This could give one possible explanation for the fixed point: the red curve lies above the blue curve to the left of the intersection, but lies below the blue curve to the right of the intersection.* In other words, since $f(0)>0$ but $f(1)<1$, there is a fixed point in the interval $(0,1)$.
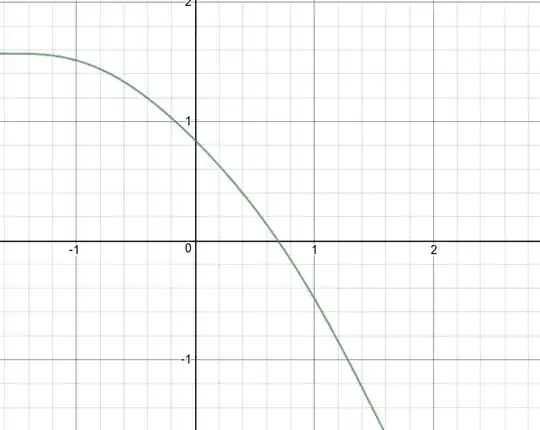
If $f(x)=x$, at the fixed point, then $f(x)-x=0$. We can name a new function, $g(x)=f(x)-x$. Hence, another interpretation of the fixed point is the value of $x$, which is a root of the function $g(x)$. The graph of $y=g(x)$ is shown in green below. This way of describing the fixed point is directly related to the formulation before, but now, the fixed point is the intersection of the green curve with the $x$-axis. And, similarly to before, since $g(0)>0$ but $g(1)<0$, there's a fixed point in the interval $(0,1)$.* Since fixed points are equivalent to a root-finding problem, it's possible to use more sophisticated root-finding algorithms to find the value of the fixed point. The algorithm in question will depend on properties of the function, such as continuity and differentiability. It may also be possible to generate an infinite series for the fixed point by the Lagrange Inversion Theorem.
The fixed point of the sequence $x_0=0,x_{n+1}=\cos(x_n)$ has very similar properties to the fixed point we've been discussing; the only real difference being the function and value in question. The fixed point of $x_{n+1}=\cos(x_n)$ is called the Dottie Number.
A simple python3 code to generate the fixed point is as follows:
import math as m
x=0
t=0
n=0
N=100
while n<N:
x=m.sin(m.cos(x))
t=m.sin(t)
n=n+1
print(x,t)
This code generates the first fixed point as $x\approx 0.6948196907307875$ and the second one as $x\approx 0.7390851332151607$. These values are listed in the OEIS as sequence A131691 and sequence A003957, respectively.
Not only are the values fixed point but, as shown in your graph, they're also attractor. Attractors are values that the system evolves towards. For both sequences, for any real $x_0$ we use, we'll approach the same fixed point.
* These statements are reliant on the fact that curves in question are continuous.
If the iterates $x_{n+1}=f(x_n)$ converge to a constant $x$, then this constant is a solution of the equation
$$x=f(x).$$
Using a numerical solver,
$$x=\sin\cos x,$$
$$x=0.6948196907308\cdots$$
Note that such a behavior is pretty common (I mean convergence to a constant) and is studied by the Fixed-Point Theorem. It is not at all specific to trigonometric functions.
As for the sequence $a_0=x,\ a_n=\cos\cos\cos\cdots x,\ n$-times, We have $\lim_{n\to\infty}a_n=V_n\implies V_n=\cos V_n\implies V_n\approx0.739...$
As for $N_s$, set $\cos\sin\cdots x=N^s$ now: $N_s=\sin N^s$ and $N^s=\cos N_s$ so $N_s=\sin\cos N_s$ thus $N_s\approx 0.694...$
