Find the Taylor series at $0$ for $f(x)=(1-x^2)^{-1/2}$

Question

Find the Taylor series at $0$ for $f(x)=(1-x^2)^{-1/2}$.

The answer given is $\sum_{k=0}^{\infty} {-1/2\choose k} x^{2k}$.

Can anyone provide a proof that gives the answer that is given?

Update: Error in answers book should be $\sum_{k=0}^{\infty} (-1)^k {-1/2\choose k} x^{2k}$

Answer 1

Let $g(x)=(1-x)^{-\frac12}$. Then

• $g'(x)=\frac12(1-x)^{-\frac32}$;
• $g''(x)=\frac12\times\frac32(1-x)^{-\frac52}$

and so on. It is easy to prove by induction that$$g^{(k)}(x)=\frac{1\times3\times\cdots\times(2k-1)}{2^k}(1-x)^{-\frac{2k+1}2}.$$In particular,\begin{align}\frac{g^{(k)}(0)}{k!}&=\frac{1\times3\times\cdots\times(2k-1)}{k!2^k}\\&=\frac{1\times3\times\cdots\times(2k-1)}{(2k)!}\\&=(-1)^k\binom{-\frac12}k.\end{align}So, the Taylor series of $g$ at $0$ is$$\sum_{k=0}^\infty(-1)^k\binom{-\frac12}kx^k$$and this implies that the Taylor series of $f$ at $0$ is$$\sum_{k=0}^\infty(-1)^k\binom{-\frac12}kx^{2k}.$$

Answer 2

Computing the binomial coefficient: $$ \begin{align} \binom{-1/2}{n} &=\frac{\left(-\frac12\right)\left(-\frac32\right)\cdots\left(-\frac{2n-1}2\right)}{n!}\\ &=(-1)^n\frac{1\cdot3\cdots(2n-1)}{2^nn!}\\ &=(-1)^n\frac{(2n)!}{2^nn!\cdot2^nn!}\\ &=\left(-\frac14\right)^n\binom{2n}{n}\tag1 \end{align} $$ Thus, the Binomial Theorem says $$ \begin{align} \left(1-x^2\right)^{-1/2} &=\sum_{n=0}^\infty\binom{-1/2}{n}\left(-x^2\right)^n\\ &=\sum_{n=0}^\infty\binom{2n}{n}\left(\frac{x^2}4\right)^n\tag2 \end{align} $$

---

$\boldsymbol{\displaystyle{\sum_{k=0}^n\binom{2n-2k}{n-k}\binom{2k}{k}=4^n}}$

It is easy to see that $\binom{2n}{n}$ is the number of strings consisting of $n$ $+$s and $n$ $-$s, and thus the number of one-step up-down paths of length $2n$ that return to their start point.

Now let's count the number of one-step up-down paths of length $2n$ that never return to their start point.

Since there are an even number of steps, the path will end at position $2k\ne0$. Isolate the part of the path that starts at the first point the path attains position $k$ (shown in red):

Reverse that part of the path and move it to the front:

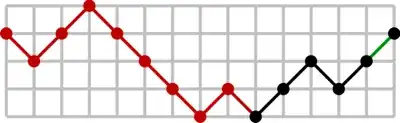
This maps any path of length $2n$ that never returns to its starting point, to a path of length $2n$ which ends up where it started.

Let's start with a path of length $2n$ that ends up where it started. If the last step is up (as shown in green), isolate the part of the path ending at the last point where it attains its minimum (shown in red). If the last step is down, isolate the part of the path ending at the last point where it attains its maximum.

Reverse that part of the path and move it to the end.

This matches paths of length $2n$ that never return to their starting point with paths of length $2n$ that end up at their starting point via a bijection. Thus, the number of paths of length $2n$ that never return to their starting point is $\binom{2n}{n}$.

Any path of length $2n$ can be uniquely written as a path of length $2k$ that returns to its starting point, followed by a path of length $2n-2k$ that never returns to its starting point. Since the total number of path of length $2n$ is $2^{2n}=4^n$, the previous counting arguments imply $$ \sum_{k=0}^n\binom{2n-2k}{n-k}\binom{2k}{k}=4^n\tag3 $$

---

Equations $(2)$ and $(3)$ show that $$ \left((1-x)^{1/2}\right)^2=\frac1{1-x}\tag4 $$ which is comforting.

Answer 3

The Maclaurin series of Power function is stated to be Binomial expansion, then for $$f(x)=(1-x^2)^{-1/2}$$ we could receive the $$f(x)=\sum_{k=0}^{\infty}(-1)^k\binom{-1/2}{k}1^{-1/2-k}\cdot(x^2)^k$$, since we have negative power, binomial theorem returns us series, particularizing above expression, we receive: $$f(x)=\sum_{k=0}^{\infty}(-1)^k\binom{-1/2}{k}x^{2k}$$ For your reference wikipedia article about Binomial theorem is attached https://en.wikipedia.org/wiki/Binomial_theorem