0

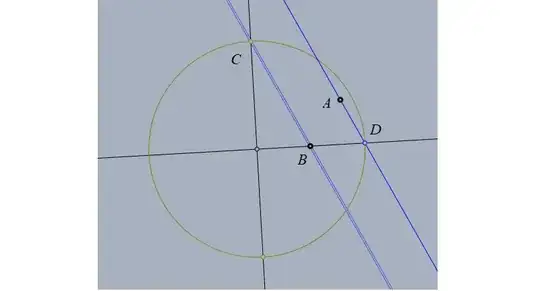
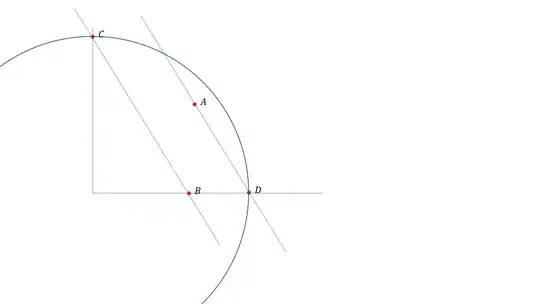
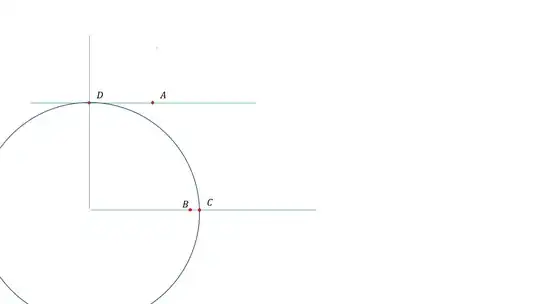
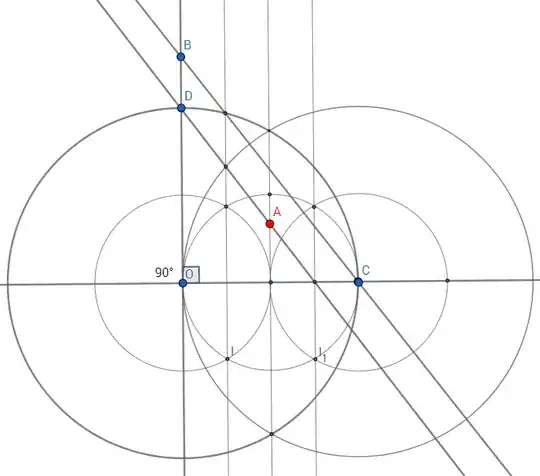
Given a right angle at $O$ (Origin), a point $B$ on one arm, and a point $A$, construct with ruler and compass a circle with center $O$, meeting the arms of the right angle at $C,\, D,$ such that $AD$ is parallel to $BC$. (par 9)

Its not so hard to construct a parallel line passing through $A$ where one side touch's a point on the radius of circle but both is alot harder. we will want the angle to be $45^°$ but I am not sure how to construct it in only nine steps where neither of the parallel lines count as a step.

This is exercie 13.18 in geometry from Hartshorne.

zoli
  • 20,452
Faust
  • 5,669
  • Which point lies on the same arm as $B$? Are $C$ and $B$ on the same arm or $D$ and $B$ on the same? – Stefan4024 Nov 21 '17 at 16:17
  • Your description is incomplete, and the description you give in the second paragraph doesn't seem to me to match the diagram in the book. (This exercise is available in the Amazon preview. – rogerl Nov 21 '17 at 16:22
  • B lies on one of the arms, A lies anywhere we wish to construct a circle st C is on the opposite arm than B is where BC is parallel to AD where D is and C lie on the arms of a circle with centre O and radius OC or OD – Faust Nov 21 '17 at 16:28
  • I took the question as is from the free old edition of the link book, and it is word for word. the second paragraph is my intuition the angle must be 45 degrees where the parallel line cuts the circle or the construction will not work. – Faust Nov 21 '17 at 16:30
  • @Faust were you able to come up with a construction based from Zoli's analytic approach? If so, could you share post it? It would be greatly appreciated! – Jeremy Cho Nov 23 '17 at 00:44
  • The book by hartshorne is a free pdf from any of those archive sites chapter 13 explains how to multiply segments, take square roots of squares etc, it is alot of work but it is construable in this way so im confident its the correct solution. the fact that it takes 9 steps is also a good indicator. i have alot of assignments and exams shortly due so i wont be able to post a complete solution for almost a month – Faust Nov 23 '17 at 13:47

3 Answers3

3

First, consider the analytic solution of the problem.

Let the coordinates of the points in the figure below be: $B=(b,0)$, $A=(u,v)$, $D=(R,0)$, and $C=(0,R)$.

enter image description here

The slope of the double line is $-\frac Rb$. As a result, the equation of the thin line is

$$-\frac Rb=\frac{y-v}{x-u}.$$

If $y=0$ then $x=R$ in the case of the thin line. Taking this into account, we get an equation for the right $R$s:

$$-\frac Rb=\frac{-v}{R-u}$$

or $$R^2-uR-bv=0.$$

The solutions are $$R_{1,2}=\frac12(u\pm\sqrt{u^2+4bv}).$$ This formula shows that the segment of length $R$ can be constructed if segments of lengths $u,v$ and $b$ are given.

See this article to learn how to multiply segments. See this answer to learn how to take square roots. Addition, subtraction, and halving must be obvious.

zoli
  • 20,452
1

A drawing of what I think is being asked, just to help others get started: enter image description here

No...wait: here's a solution (to what I think cannot be what the problem intended):

Draw a (green) line through $A$ parallel to the green leg containing $B$; let its intersection with the other leg be $D$. Draw a circle of center $O$ and radius $OD$, meeting $B$'s leg at location $C$. Now $BC$ is the green leg, and $AD$ is parallel to it.

enter image description here

John Hughes
  • 93,729
  • I was going to post a picture was just uploading it, your first drawing is fine but a can be inside as well. your solution i dont follow from your bottom picture clearly line AD is not parallel to line BC? for one they interect so they cannot possibly be parallel. – Faust Nov 21 '17 at 16:53
  • You're completely right -- I had in my head "AC parallel to BD", which isn't what's needed at all. I'll delete that second bit. THanks! – John Hughes Nov 21 '17 at 16:56
  • And now I've re-fixed that so that it's "correct", if you believe my interpretation of the problem (which is that $C$ is not constrained, by what's asked, to lie on the other leg from $B$). – John Hughes Nov 21 '17 at 17:58
  • Lmao that's a hilarious solution! – Faust Nov 21 '17 at 18:04
  • That's what I thought....but I have a hard time believing it's what Hartshorne intended. My recollection is that his problems were never easy. – John Hughes Nov 21 '17 at 18:08
0

I think the answer is the following:


enter image description here

Darío A. Gutiérrez
  • 3,863
  • Looks like you drop a perp from $A$ to bottom leg, draw circle at $O$ through intersection point; reflect that across the perpendicular you dropped, and call the new circle-center $C$. (I.e., OC is twice $OK$, where $K$ is the foot of the perpendicular). The you draw a circle with center $O$ and containing $C$. But what happens if you raise $A$ about 4 inches in your picture? Nothing in the construction of $C$ changes, but $AD$ is no longer parallel to $BC$. I must be missing something. – John Hughes Nov 21 '17 at 17:00
  • Sorry this can't be correct, the choice of B is arbitrary and nothing in the construction is dependent on the choice of B, he must be picking C s.t the line BC has A contained in it when thats possible? – Faust Nov 21 '17 at 17:24