Your specific question related to secant method has already been answered here, so I will instead address you more general question, i.e., why are some formula inferior to others.
While computational speed is important, it is completely secondary to meeting the accuracy goal for all possible input. Two different formula can be equivalent, yet differ wildly when evaluated using finite precision arithmetic.
A good example are the functions $f$ and $g$ given by
$$f(x) = \sqrt{4 + x^2} - 2, \quad g(x) = \frac{x^2}{2 + \sqrt{4 + x^2}}.$$
It is trivial to verify that $f(x) = g(x)$ for all $x$, yet when evaluated using, say, IEEE double precision floating point arithmetic, profound difference immediately emerge. For small values of $x$, the graph of $f$ is shaped like a staircase, while the graph of $g$ has the correct parabolic shape.
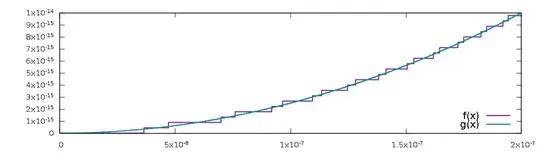
Moreover, for $|x| < 2^{-26}$, the computed value of $f$ is $0$, despite the fact that $f(x) > 0$ for all $x \not = 0$. In on the set $0 < |x| < 2^{-26}$ the relative error is 100%. The function $g$ does not suffer from this problem.
As in the case of the secant method, the departure from the mathematical reality is due to an ill conditioned step in the computation of $f$. In general, the subtraction $d = a - b$ of two real numbers is an ill conditioned problem, when $a$ and $b$ are close to each other. This is a phenomenon which is explained in some detail here.
In contrast, the addition of positive real numbers, multiplication and division of real numbers as well as the computation of square roots are all well conditioned problems. Therefore, the formula for $g$ can be evaluated accurately. However, since $\sqrt{4 + x^2} \approx 2$ for $x \approx 0$, the subtraction dramatically magnifies the relative importance of the rounding errors committed when computing $\sqrt{4 + x^2}$.
In general, we have to rewrite expressions to avoid steps which are ill conditioned.
