In the general case, it may be difficult to obtain a closed-form solution (cf. comments by @LutzL). However, it is not so difficult to have qualitative information in the general case, and to compute a closed-form solution in the case $g=0$. This reference solution could be used to validate the numerical method (cf. @caverac answer).
Qualitative analysis. To get a first insight of the solution, one can linearize the system in the vicinity of its equilibrium positions (cf. Hartman-Grobman theorem). If the time-evolution is set to zero, then one has $v_x = 0$ and $v_y = \sqrt{g/k}$. The Jacobian matrix $J_f$ of the mapping $\frac{\text{d}}{\text{d} t}(v_x,v_y) = f(v_x,v_y)$ is
$$
J_f = -\frac{k}{\sqrt{{v_x}^2 + {v_y}^2}}
\left(
\begin{array}{cc}
2{v_x}^2 + {v_y}^2 & {v_x}v_y \\
{v_x}v_y & {v_x}^2 + 2{v_y}^2
\end{array}
\right) .
$$
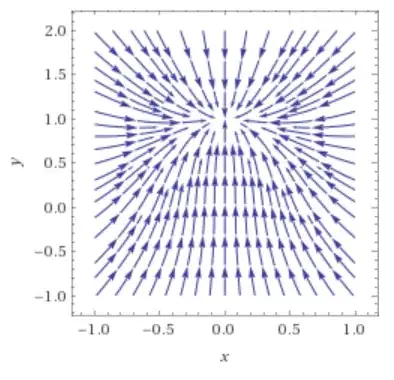
Therefore, if $k>0$, the equilibrium position $(0,\sqrt{g/k})$ is stable, and the solution will be attracted by the equilibrium position. This can be viewed on the following phase diagram, where $k=g=1$:
Analytical solution: case $g=0$, $k>0$. In the present case, the origin and the stable equilibrium coincide. Multiplying the first equation by $v_x$ and the second equation by $v_y$ and summing both equations, one has
$$
\frac{\text{d}}{\text{d}t} \left( {v_x}^2 + {v_y}^2\right) = -2k ({v_x}^2 + {v_y}^2)^{3/2} .
$$
Therefore,
$$
{v_x}(t)^2 + {v_y}(t)^2 = \frac{c_1}{\left(1 + k t \sqrt{c_1}\right)^2}\, ,
$$
where $c_1 = {v_x}(0)^2 + {v_y}(0)^2 \geq 0$. Injecting this in the first equation, one has
$$
\frac{\text{d}v_x}{\text{d}t} = - \frac{k v_x \sqrt{c_1}}{1 + k t \sqrt{c_1}} \, ,
$$
with solution
$$
v_x(t) = \frac{c_2}{1 + k t\sqrt{c_1}} \, ,
$$
provided that $c_2 = v_x(0)$. Lastly, we deduce $v_y$ from ${v_x}^2 + {v_y}^2$ and $v_x$, or from the fact that $v_x$ and $v_y$ play symmetric roles in the equations.
The case $g>0$, $k=0$ can be solved by hand easily too.
