4

Is it possible to derive a probability density function $P(d,L)$ which gives probability of having a point to point distance $d$ on a $2D$ square lattice of size $L$ or at least it's asymptotic behavior ?

user2528893
  • 41
  • It makes more sense to ask how many distinct distances exist between points of the lattice. A simple upper bound is $\frac 12(L+2)(L+1)$ which is the number of pairs $(a,b)$ with $0 \le a,b \le L, a\le b$. From that we would have to subtract the number of distances that are represented twice, as $5$ can come from $(0,5)$ and $(3,4)$ and $\sqrt {65}$ can come from $(1,8)$ and $(6,7)$. I don't have a good way of estimating the last part. – Ross Millikan Nov 19 '17 at 18:43
  • Thanks for the answer, but isn't total number of distinct distances simply $\binom{L^2}{2} = \frac{(L^2)(L^2-1)}{2}$ ? – user2528893 Nov 19 '17 at 18:55
  • No because many of them are the same. Any pair of neighboring points gives a distance of $1$, for example. I am choosing the offsets horizontally and vertically. – Ross Millikan Nov 19 '17 at 20:33
  • Caloculations show a very spiky probability distribution for all $L \lt 7$. I doubt any nice distribution will emerge for larger $L$. Have you attempted any simulations? – Jens Nov 20 '17 at 22:27
  • This question related to this. When I looked at Mathai's paper, he generalized results from the squares over reals from Ghosh. If an exact distribution was found, I wonder if the 3D version could be solved in a similar manner. – Teg Louis Jul 08 '23 at 01:16

1 Answers1

2

Two lattice points which have a horizontal (or vertical) distance of $a$ and a vertical (or horizontal) distance of $b$, will have a point to point distance of $$d(a,b) = \sqrt{a^2 + b^2}$$

In an grid of $L \times L$ points, where $ a \lt L$ and $b \lt L$, there is a nice formula for the number of instances of the distance $d(a,b)$. For a given $a$ and $b$, where $a \ge b$, the number of instances of the distance $d(a,b)$, is $$ n = \begin{cases} 2(L-a)(L-b), & \text{if $b=0$ or $b=a$} \\ 4(L-a)(L-b), & \text{otherwise} \end{cases} $$ Since we know the total number of instances of all possible distances is $\binom {L^2}{2}$, it seems we can directly compute the probability of a given distance for a given lattice size.

However, as Ross Millikan pointed out, some distances can be generated in more than one way, i.e. for some distances $d(a,b) = d(e,f)$ where $(a,b) \ne (e,f)$. The distances where this occurs (or rather the square of those distances) can be seen here.

No formula for these distances appears available. Using the formula above, it is however fairly easy to make an algorithm which computes the probabilities. I did it by running through all possible values of $a$ and $b$ for a given grid size $L$, finding the distances which could be arrived at for different $a$ and $b$ and adding the instances for these together.

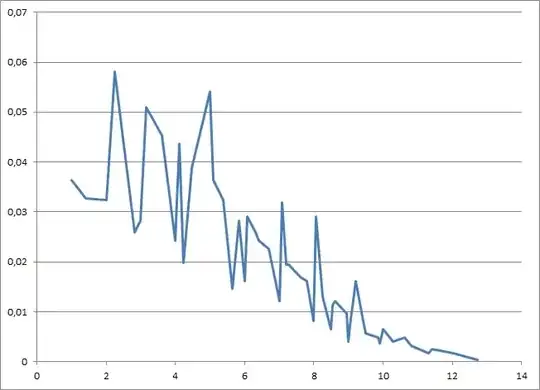
Below is a graph showing the probability distribution for $L=10$

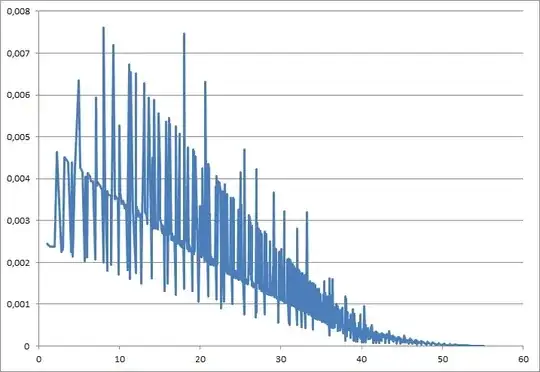
enter image description here

And here is the distribution for $L=40$

enter image description here

There seems to be an asymptotic nature to this.

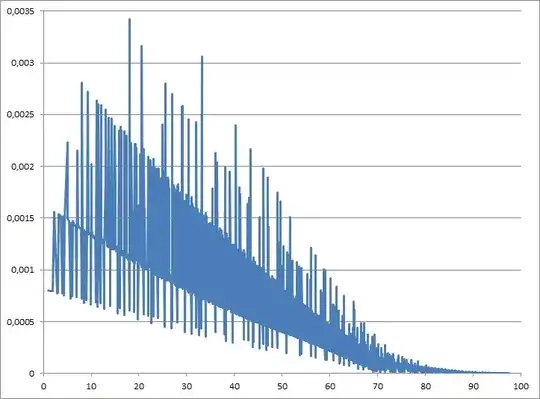
enter image description here

The above is for $L=70$. The extra large spikes occur where a distance can be generated in more than one way.

Jens
  • 5,686
  • 2
  • 20
  • 38